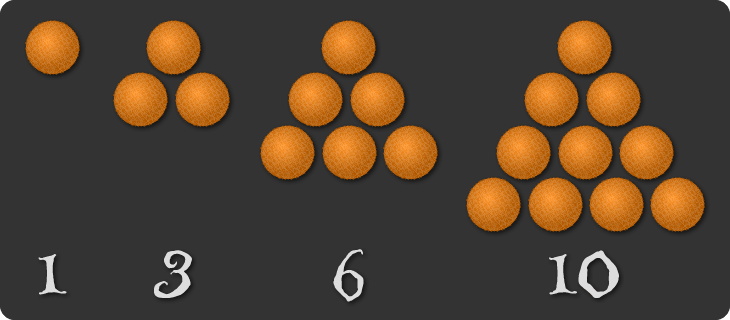Navigate using the Keyboard arrows or click anywhere on the slide to show the toolbars for more options.
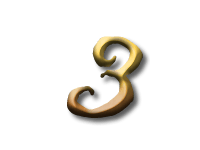
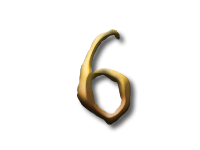
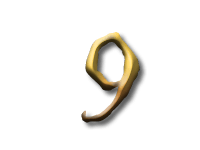
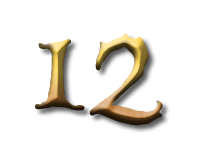
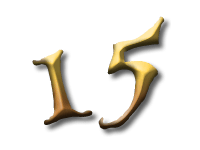
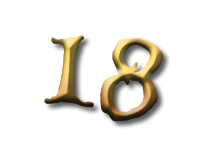
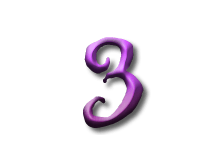
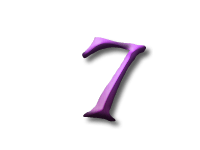
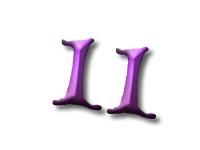
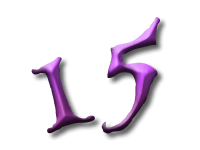
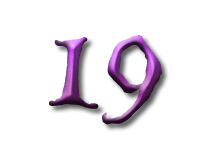
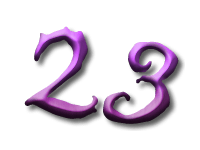
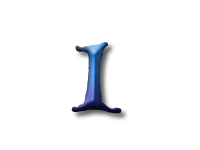
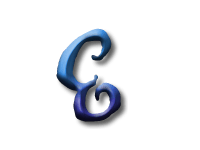
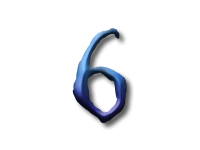
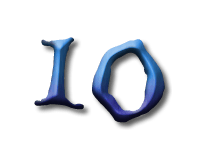
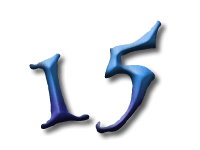
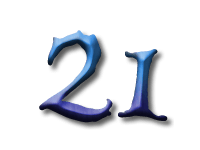
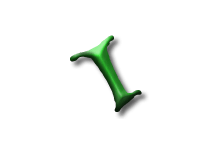
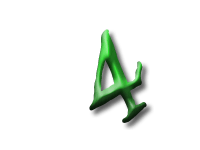
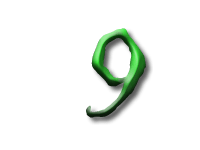
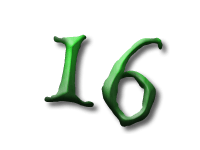
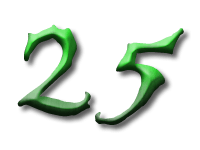
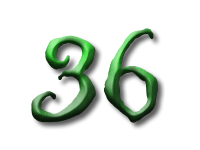
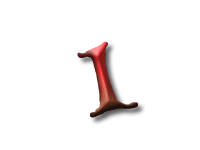
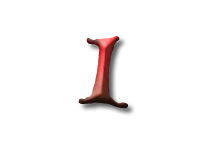
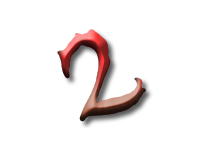
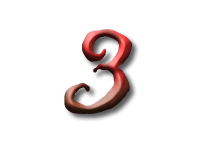
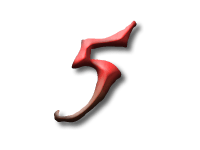
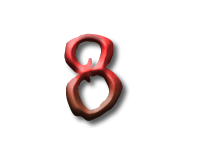
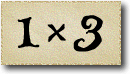
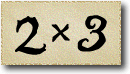
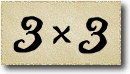
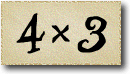
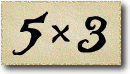
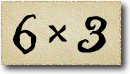
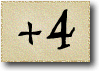
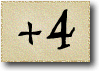
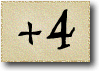
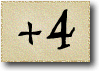
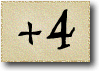
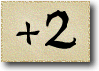
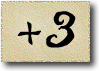
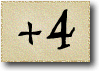

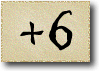
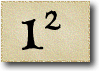





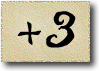

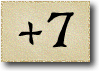
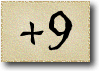
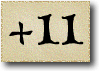
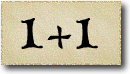
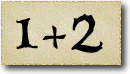
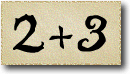
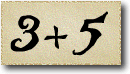
As Alice falls down the rabbit hole, she sees many different numbers flying around. And they always appear in particular patterns – these are called sequences. Can you find the pattern in these five sequences?
In the first sequence the numbers are the multiples of three: and so the difference between two consecutive numbers is three.
In the next sequence the difference between two consecutive numbers is four. But since the first number, 3, is not divisible by 4, none of the others are.
In this sequence the difference between consecutive numbers are increasing integers: 1, 2, 3, and so on. These numbers are called the triangle numbers.
This is because if you were to build triangles out of, say, oranges, you would need precisely this sequence of numbers. Every new row has one more orange than the previous one, so we have to add the next bigger integer.
And here we have the square numbers: 1 squared is 1, 2 squared is 4, and so on.
There is a second way to calculate the square numbers: we start with 1 and keep adding the next odd number.
The final sequence is called the Fibonacci sequence. We start with two 1s and every new number is the sum of the two previous numbers.
Remember these five sequences, because we will see them again in this slideshow.










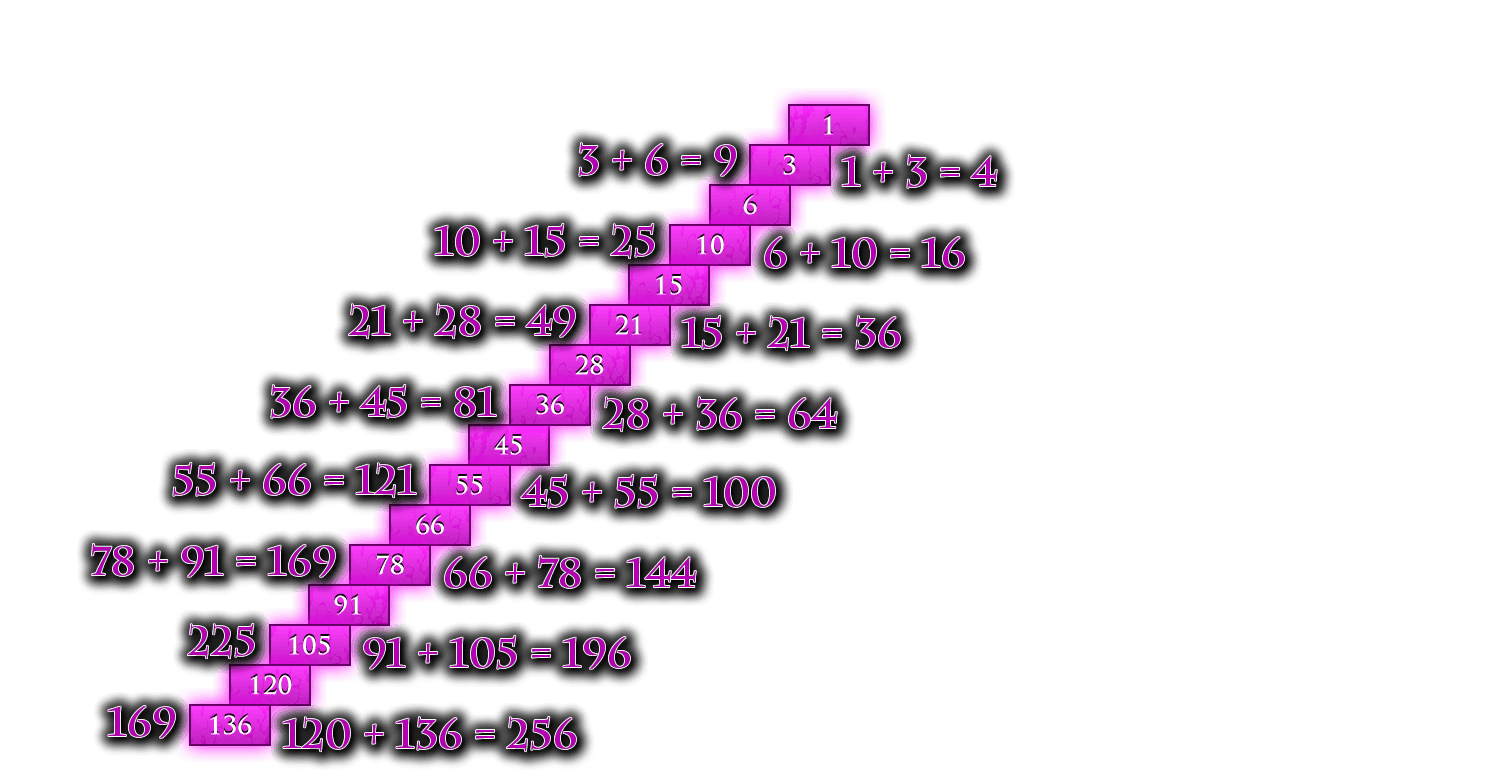
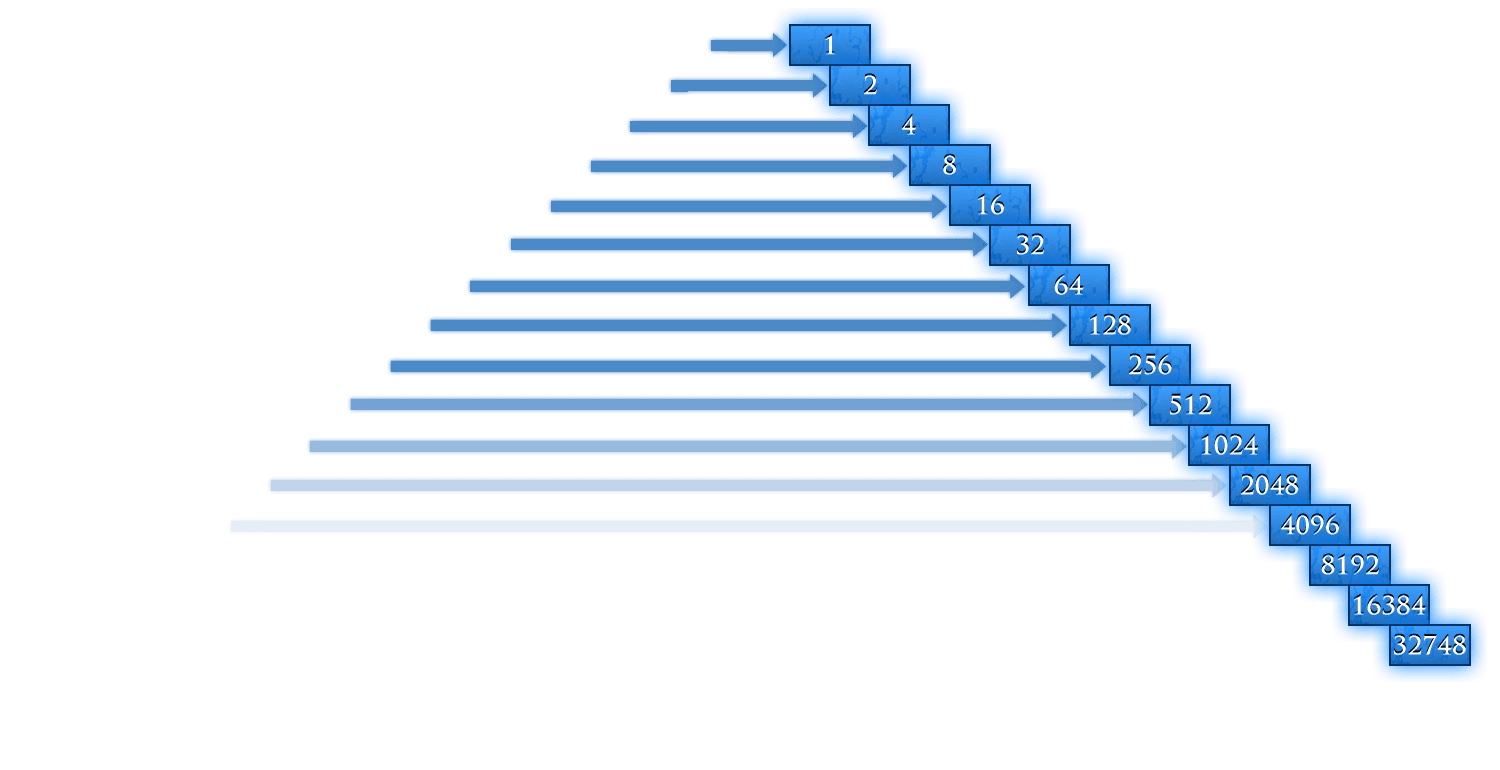
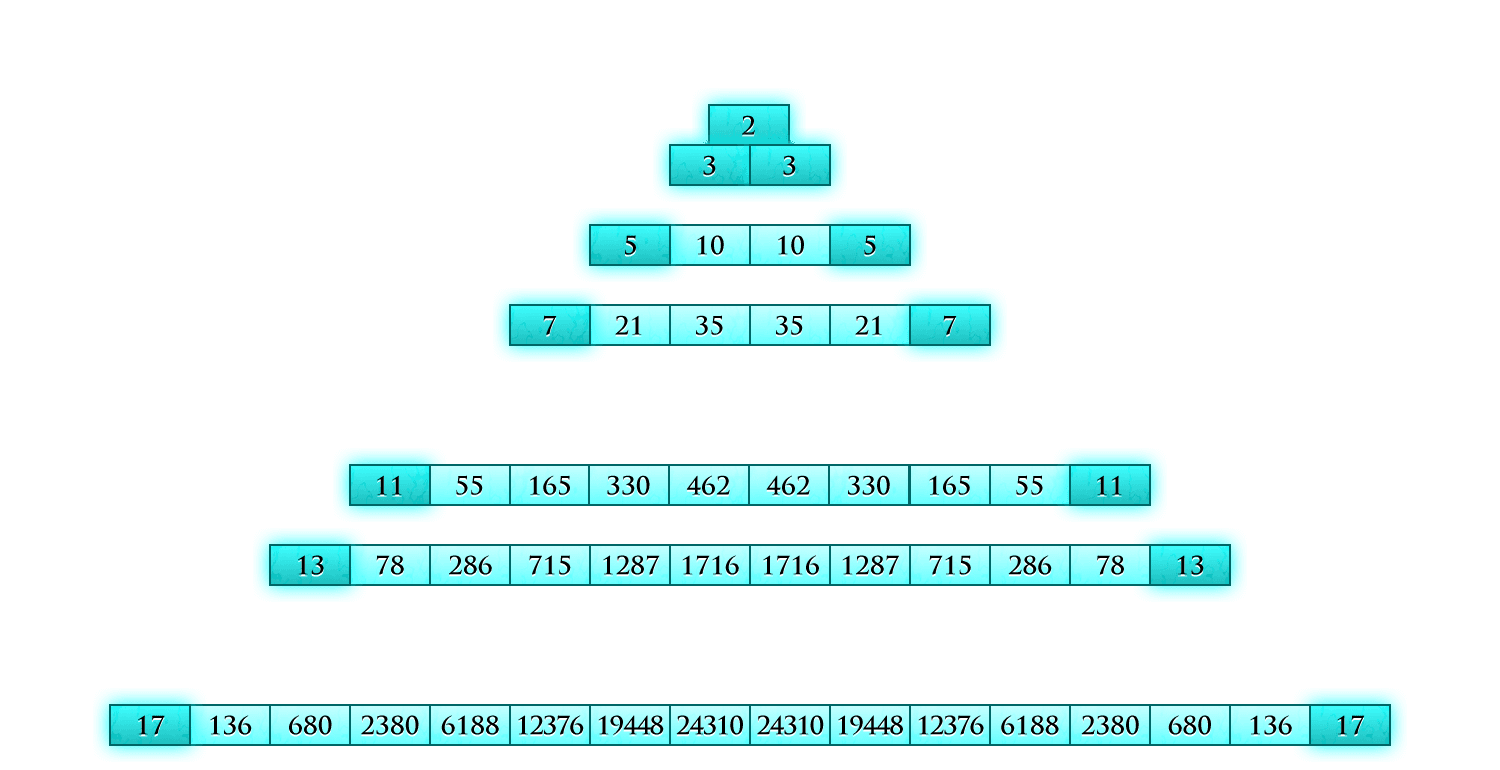
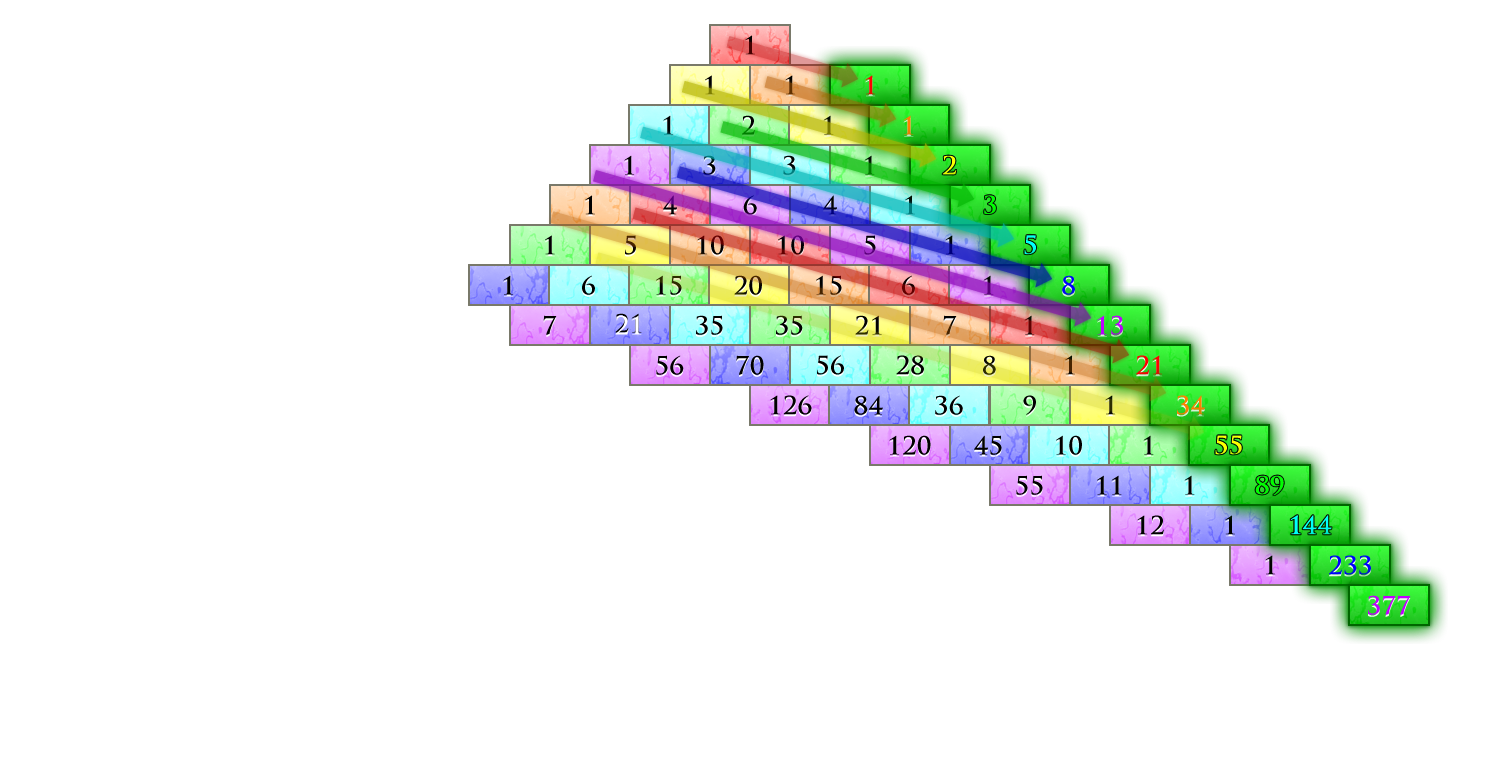
Alice hits the stone floor at the bottom of the rabbit hole. As she looks around she notices that the tiles are not simply black and white, they all have small numbers in them. And an inscription reads: Pascal's Triangle.
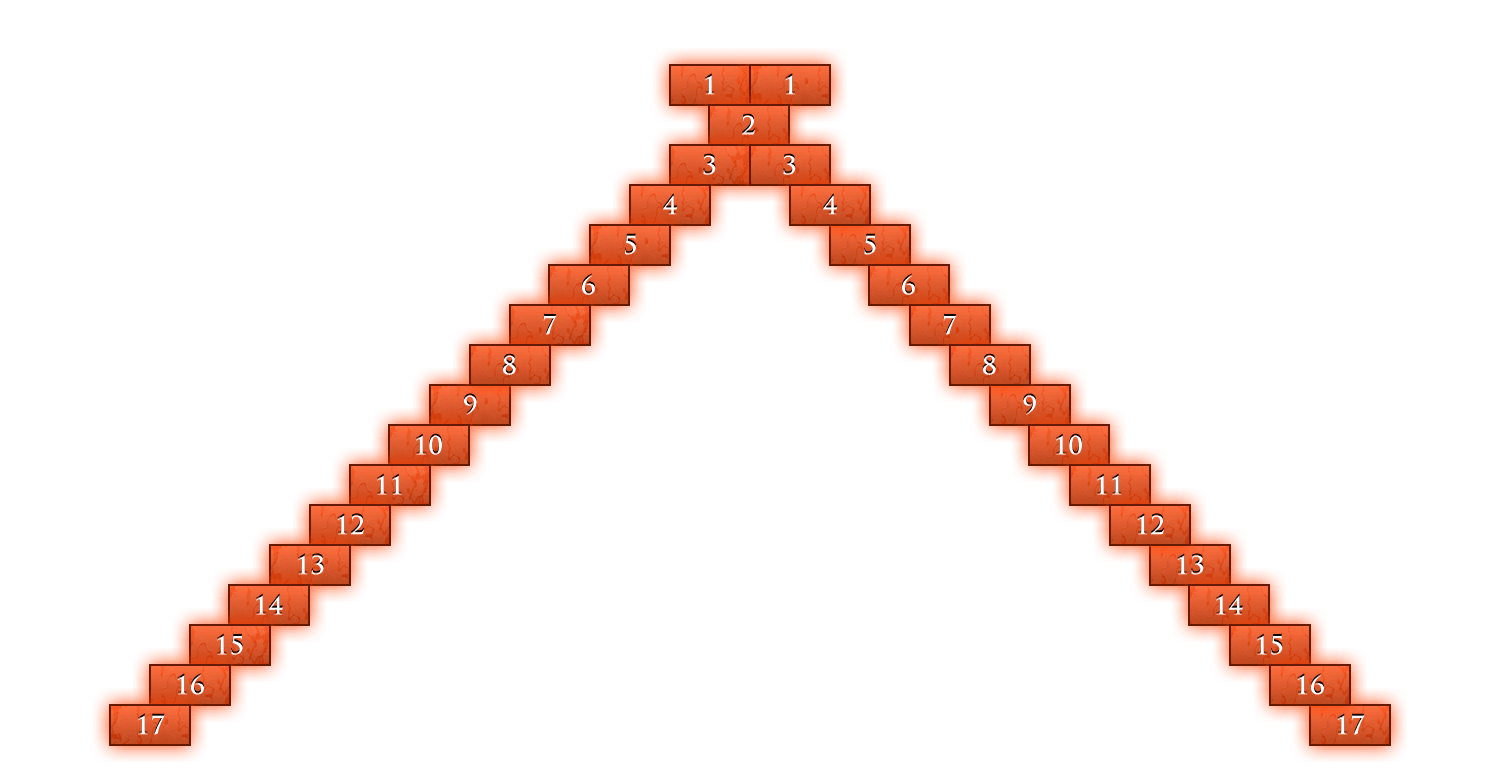
Alice notices that the triangle starts in one corner of the room but goes on forever in the other direction. And every new row is a bit bigger than the previous one. "This must be an awfully big room", she thinks.
The numbers also seem to get bigger, except along the edge where there are only ones. But Alice notices a pattern: every new number is the sum of the two numbers above it.
Can you find the next one or two rows of this triangle?
There are many mysterious patterns and secrets in this triangle. Before continuing, have a look at the numbers and try to find some of them.
Suddenly Alice sees a couple of bright buttons at the wall, and whenever she presses one of them, some tiles on the floor light up.
The first button lights up the outer diagonals which consist only of ones.
The second button lights up the second diagonals: and these are the integers 1, 2, 3, and so on.
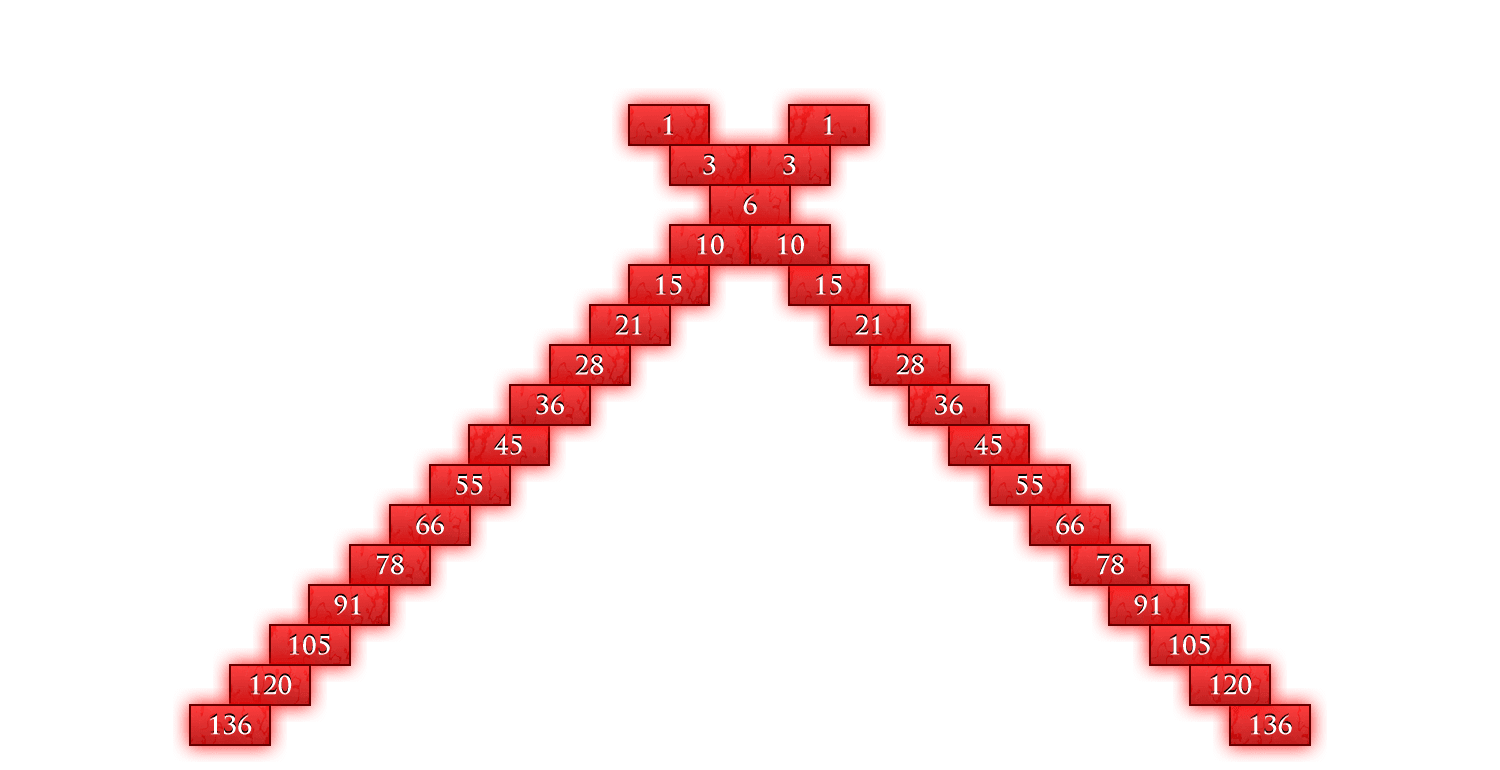
The third button shows the third diagonals. This is one of the sequences we saw before and they are called the triangle numbers.
The fourth button also lights up the triangle numbers, but this time in pairs. And when you add up consecutive triangle numbers you get the sequence of square numbers.
Can you explain why that happens? Think about it geometrically!
And there are still more buttons left, more patterns to find in this mysterious triangle. The fifth button reveals a new diagonal in which every number is the sum of all cells in that row. In the third row, for example, 1 + 2 + 1 = 4. And in this new diagonal, every number is twice the previous one. 1 × 2 = 2; 2 × 2 = 4; 4 × 2 = 8 and so on. These of numbers are called the Powers of Two.
The next button highlights all rows in which the second number is a prime number. And Alice notices that all numbers in between are divisible by that prime. Does it work with any numbers which are not prime?
The final button suddenly shows many different cells in different colours. We are adding up the cells along certain "shallow" diagonals. And the results are 1, 1, 2, 3, 5 and so on – another sequence we already know: every number is the sum of the previous two. Remember these numbers because we will see them again…
You should think about each of these patterns and try to explain where it comes from.
Pascal's Triangle not only knows about countless patterns and sequences but appears in many different parts of mathematics. And there are many more secrets not shown so far, waiting to be explored by you.
Alice looks around the room and on a glass table she finds many glasses in different colours. And there is a sign saying "Put me on". She is curious and does put on the first pair of glasses…


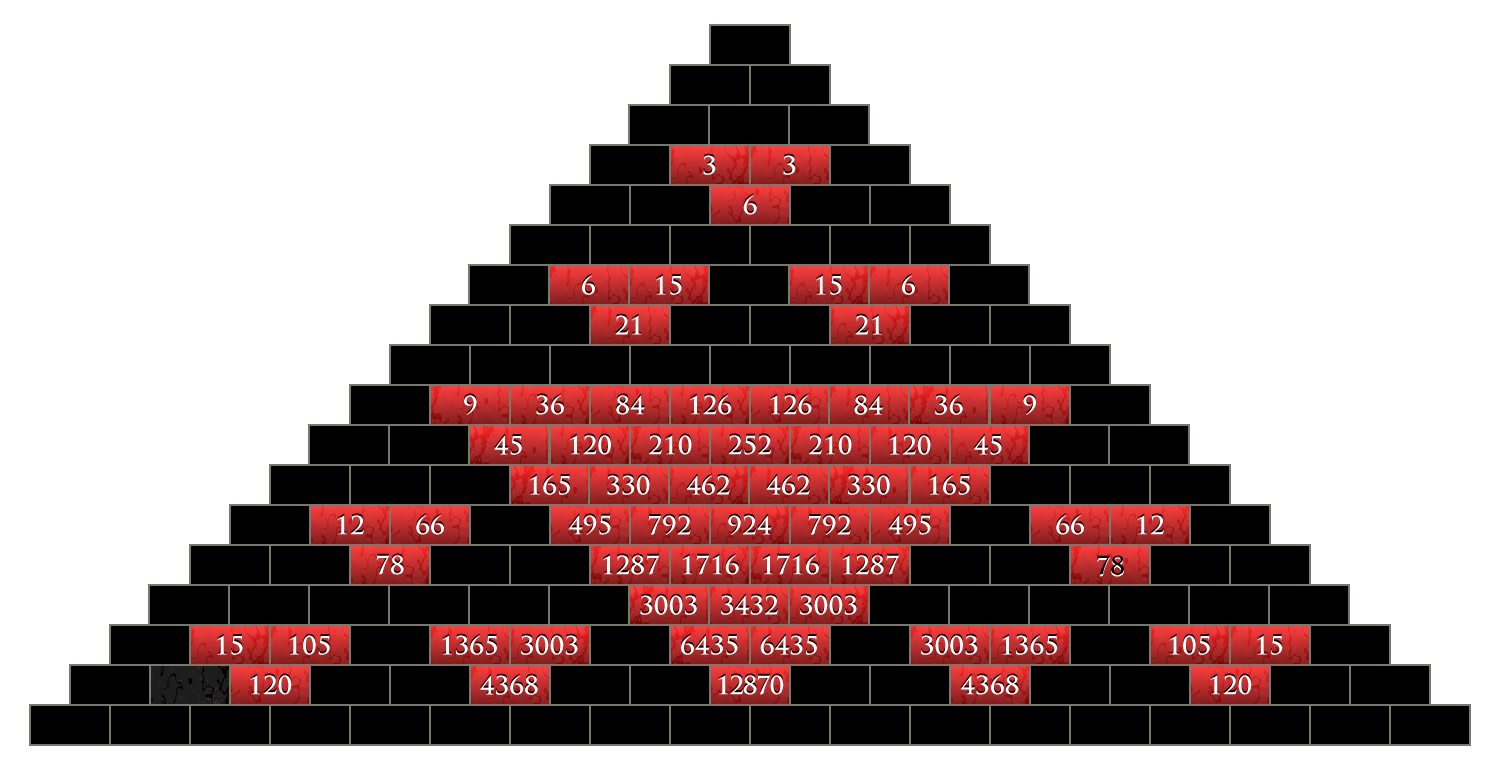
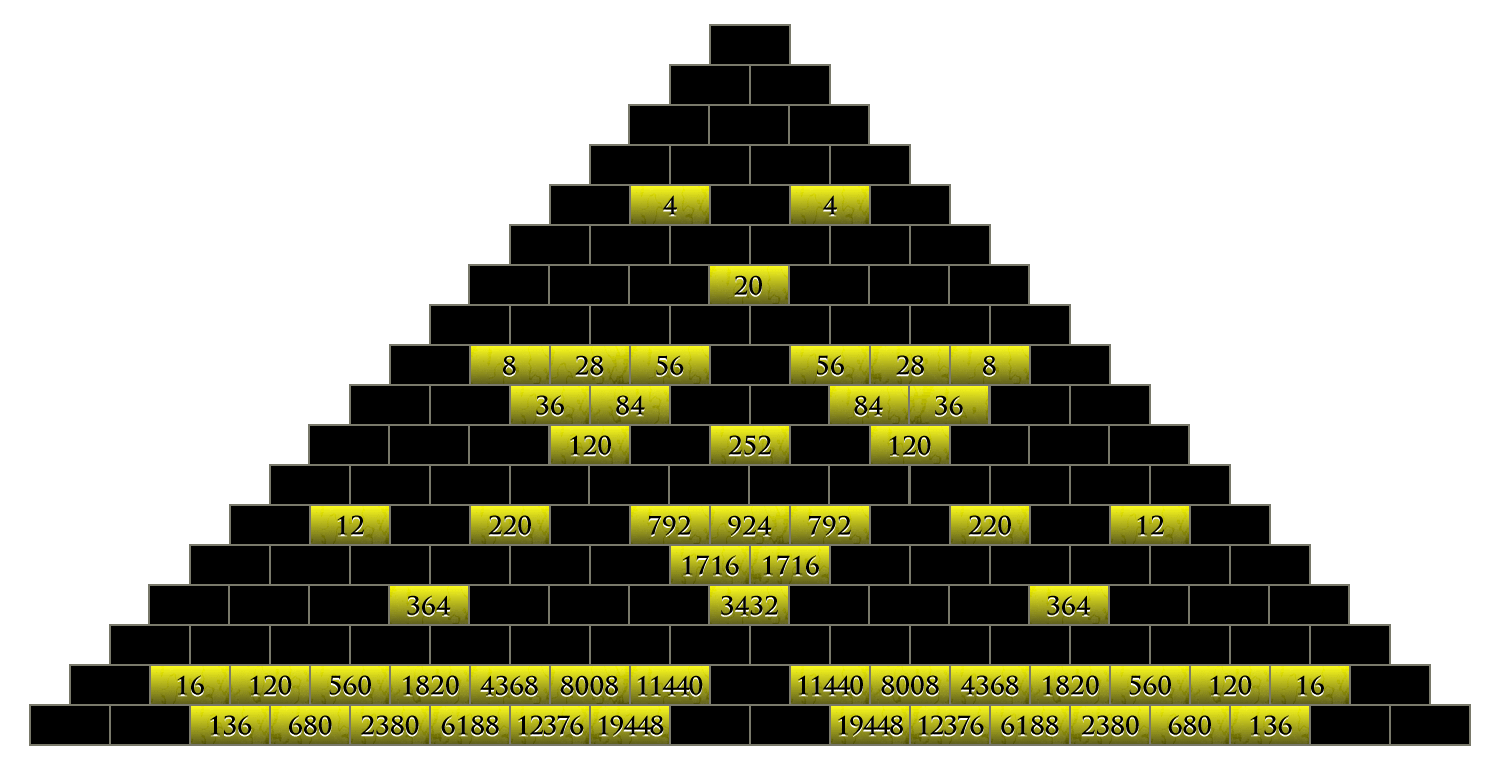
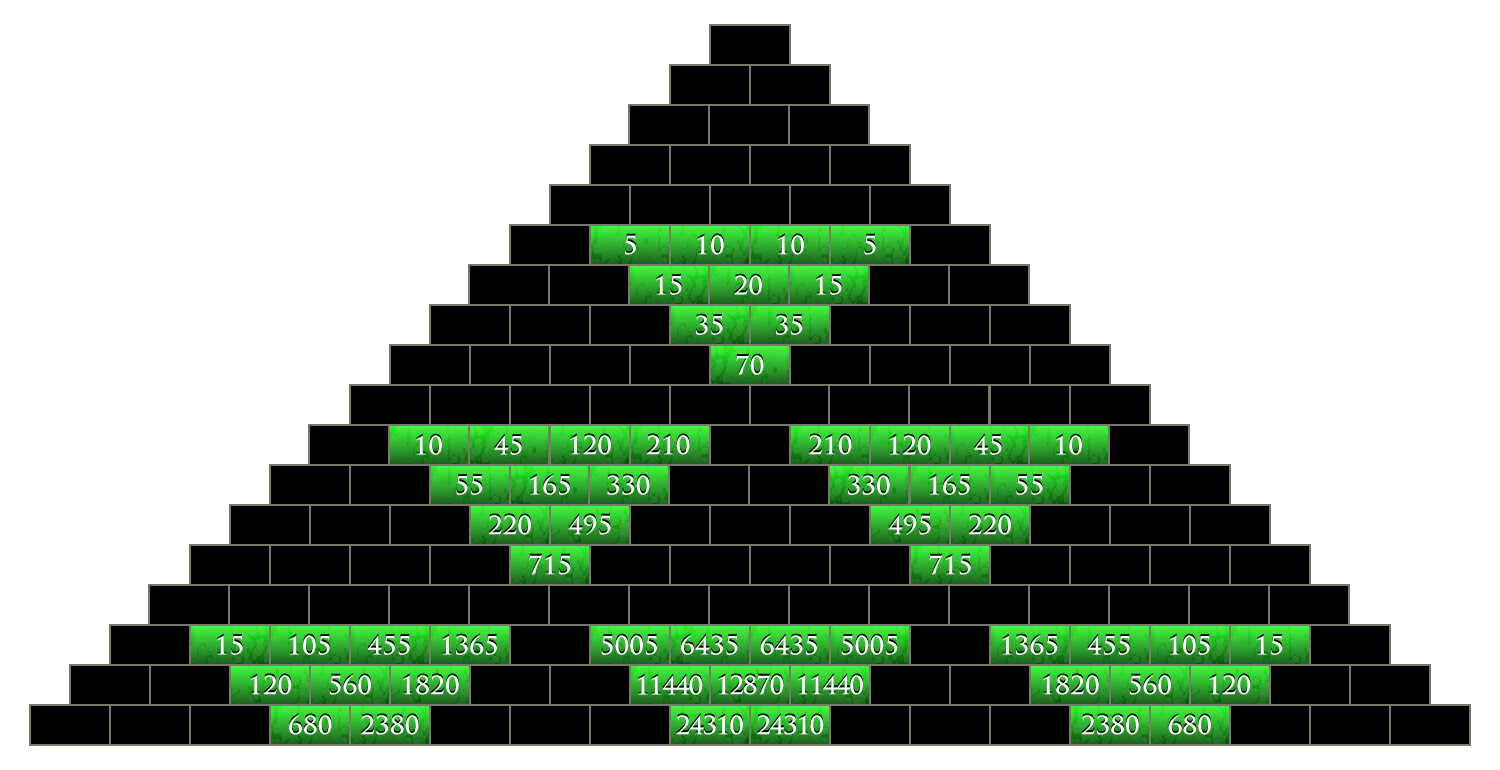




As Alice looks through the first pair of glasses, suddenly many of the tiles on the floor disappear and she seems to float in mid-air. Only those remain which are divisible by 2. But these are not located randomly: they form many small and bigger triangles!
When Alice takes off the glasses, everything is back to normal. Each of the glasses corresponds to a particular number.
The red glasses, for example, show only those numbers divisible by 3. And again thy appear in triangles which get bigger and bigger.
Alice puts on the yellow pair of glasses and now she sees only those numbers divisible by four.
And finally, the green glasses show her only those numbers divisible by five.
Think about all these patterns and try to explain where they are coming from. You can also download a big copy of Pascal's triangle and colour it in yourself: for example those numbers divisible by six or seven.
When Alice leaves the curious room, she meets someone even more amazing than what she saw before: a fractal. A Fractal is a geometrical shape which copies itself again and again at smaller scales. You can zoom in forever and will always find new, smaller copies of the original shape.
Fractals have fractional dimensions, hence the name. You could imagine that in 2- or 3-dimensional space there simply isn't enough space for that many repetitions, so they need dimensions like 2.4, 3.6 or log23.
This is of course very hard to believe but can be proved using mathematics. On the following slides we will see how to construct simple Fractals ourselves.








One of the simplest fractals is the Sierpinski triangle. We start with a plain triangle and cut out a smaller triangle in the centre.
We do the same with the four remaining triangles.
And again, and again, forever and ever.
Notice that the smaller triangles all look exactly the same as the entire big triangle. We therefore say that Fractals are self-similar.
If you remember the coloured patterns we saw in Pascal's triangle, you will notice that the Sierpinski triangle looks very similar.





Suddenly it starts snowing and Alice discovers that the snowflakes are also fractals. Again we start with a triangle and add smaller triangles to each side.
And again, and again, until we get a beautiful snowflake: the Koch snowflake. In this case, not the shape itself, but its border is self-similar.
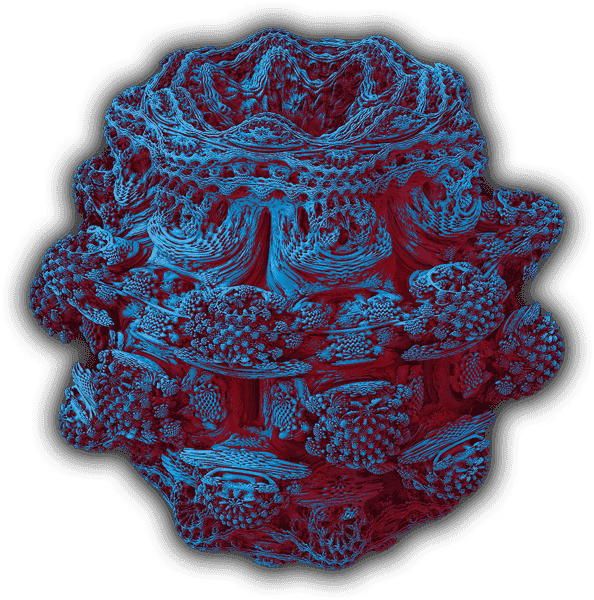
One of the most famous and most intriguing fractals is the Mandelbrot Set, named after the French mathematician Bernoît Mandelbrot (1924 – 2010). When rotated by 90° it looks a bit like a person, with head, body and two arms. And like before, we can zoom in forever, finding more and more beautiful patterns…



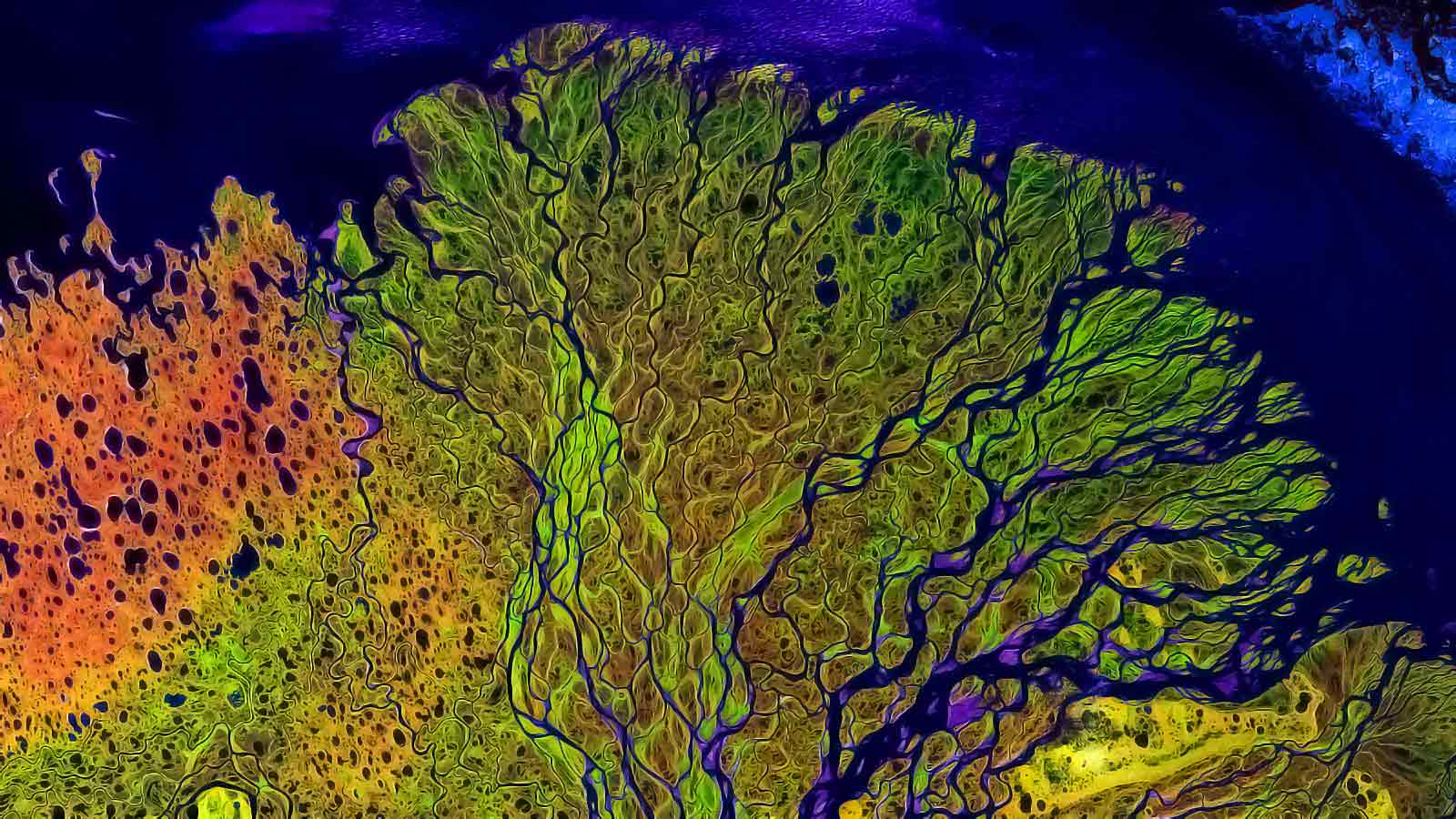




In real life, Fractals can't exist. If you zoom in further and further, you will eventually arrive at atoms and molecules – and there you have to stop. But there are many examples in nature of shapes that look almost like fractals: Vegetable, flowers and trees…
…crystals…
…coast lines…
…river networks…
…cloud formations…
…cracks in glass…
…or ice crystals.
And here in Fractalland there even is a Mandelbrot Island!







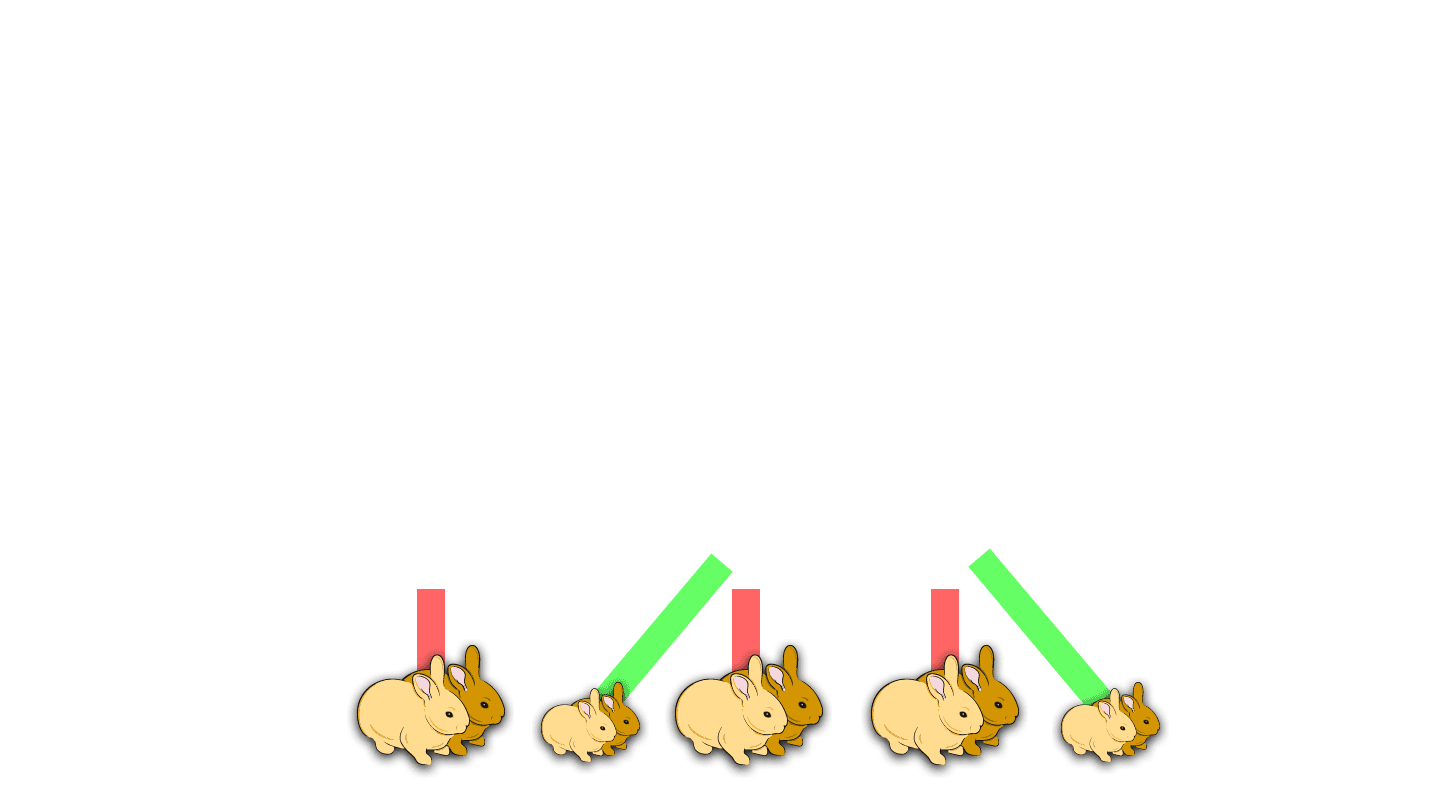



After walking through a small forest, Alice comes to a big tea party of a rabbit family. And they tell her how the family evolved.
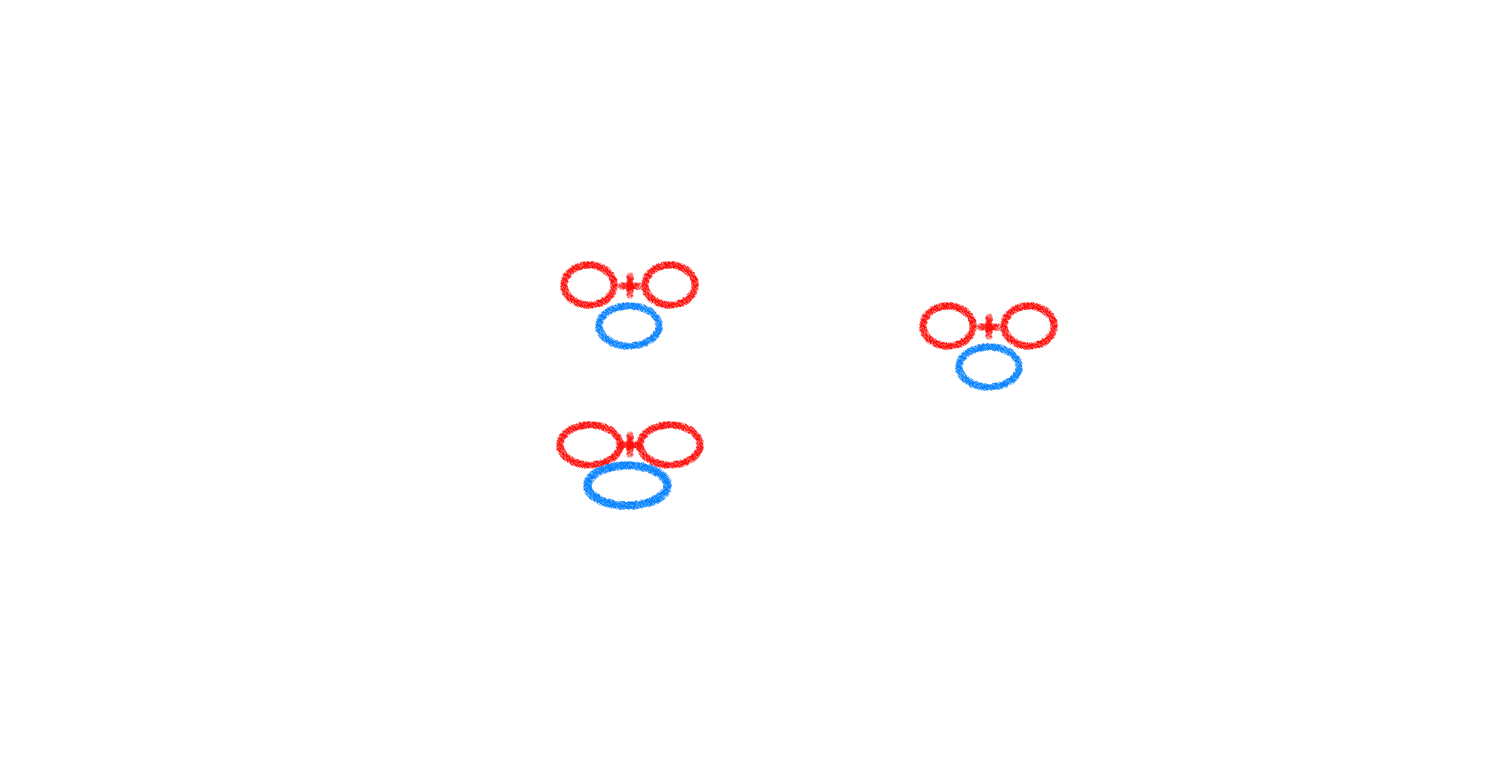
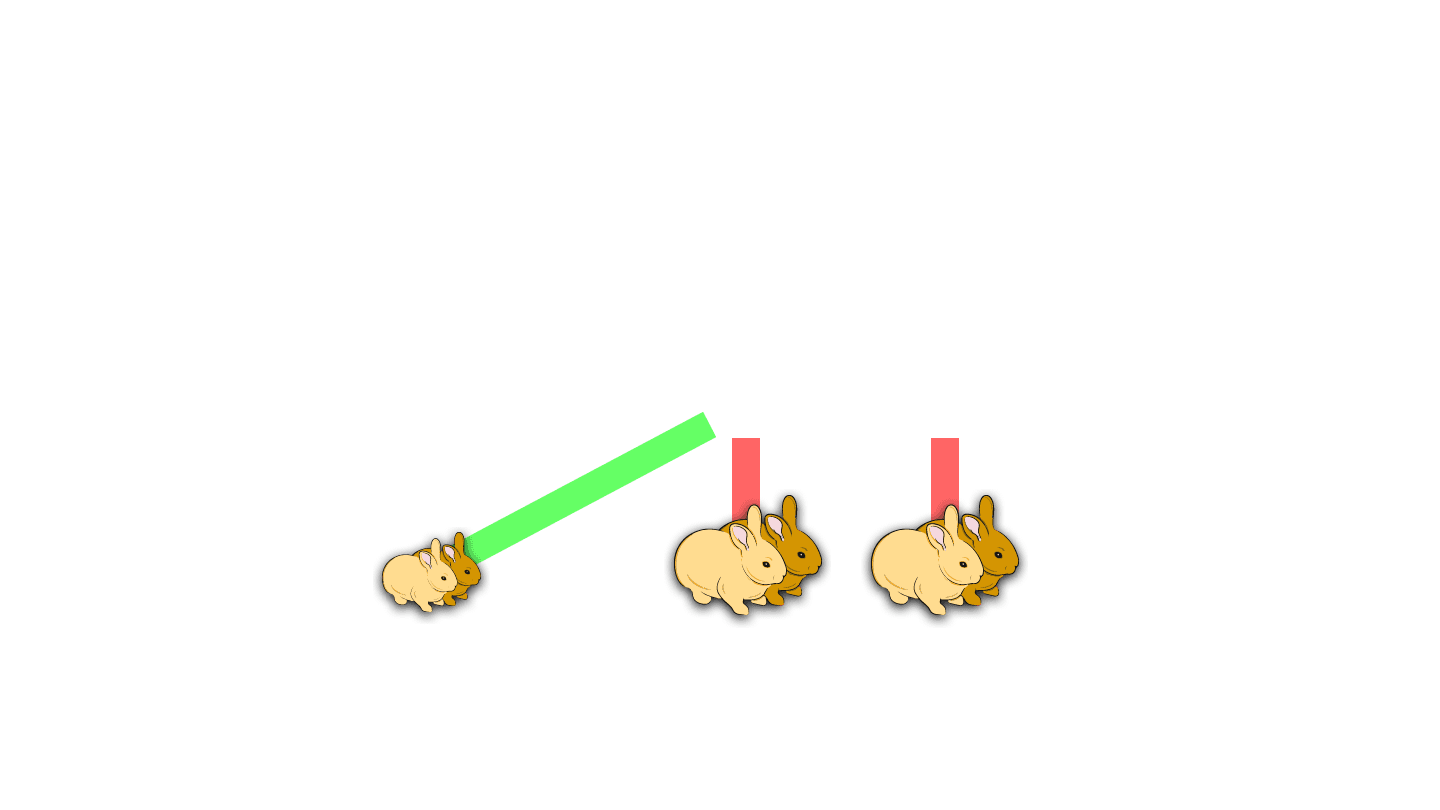
It all started with a pair of small rabbits being born in Wonderland.
After a year, they had grown up and after another year, they had children themselves: again a boy and a girl.
After another year, they had another pair of children, while their first pair had grown up.
And after another year, they had a third pair of children and their very first pair of children also gave birth to a new pair.
If we add up the number of rabbit pairs in every year we get an interesting sequence: 1, 1, 2, 3, 5, and so on.
We saw this sequence of numbers before: every new number is the sum of the previous two. The next number, for example, would be 3 + 5 = 8. They are called Fibonacci Numbers, named after the Italian Mathematician Leonardo Fibonacci.








Fibonacci Numbers appear everywhere in nature: such as pinecones or sunflowers.
If you count the number of spirals in Pinecones or Sunflowers, it will almost always be a Fibonacci number. We know that 8 is a Fibonacci number, and you can check that 34 is one as well.
If you count in the opposite direction, you get another number: but again a Fibonacci number.
Of course nature doesn't know about Fibonacci numbers: they just happen to come out of natural processes, such as growing plants or growing rabbit populations.








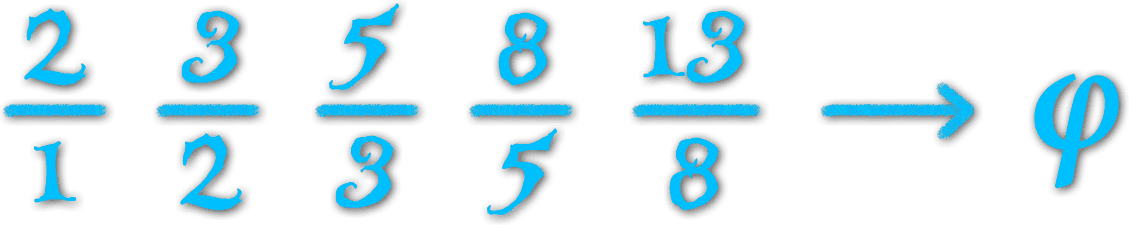

Now let us draw some squares with Fibonacci number side lengths.
If we connect the corner points we get a perfect spiral –
– another shape that appears everywhere in nature.
The proportions of our rectangles were the ratios of consecutive Fibonacci numbers. These form another sequence which gets closer and closer to a number we call Phi – or the Golden Ratio.
Some believe that the Golden Ratio is a particularly beautiful proportion, and that's why it is often used in architecture and art.
And while we found the golden ratio using a sequence of fractions, the golden ratio itself can't be expressed as a simple fraction. It is an infinite decimal number without any pattern or repetition.