Overview and Objective
In this lesson, students explore the infinite sums of different fraction sequences using geometric approximations.
Warm-Up
Invite students to work on the following sums in groups.
Let each group share their work. It might be worth sharing as a class any strategies like shortcuts or patterns that students noticed while finding the sums.
Some students may realize the general pattern of the sum, and be able to write as an expression while some simply add them up. Share both ideas.
for the sum is
for the sum is
for the sum is
for the sum is
You can use this canvas to demonstrate the sum of the powers of s on the coordinate plane.
You may want to copy and paste each sum to add one more step, then drag the blue arrow onto the coordinate plane to show its value. You may discuss with students that the sum is getting closer to 1 each time we add another power of 1/2.
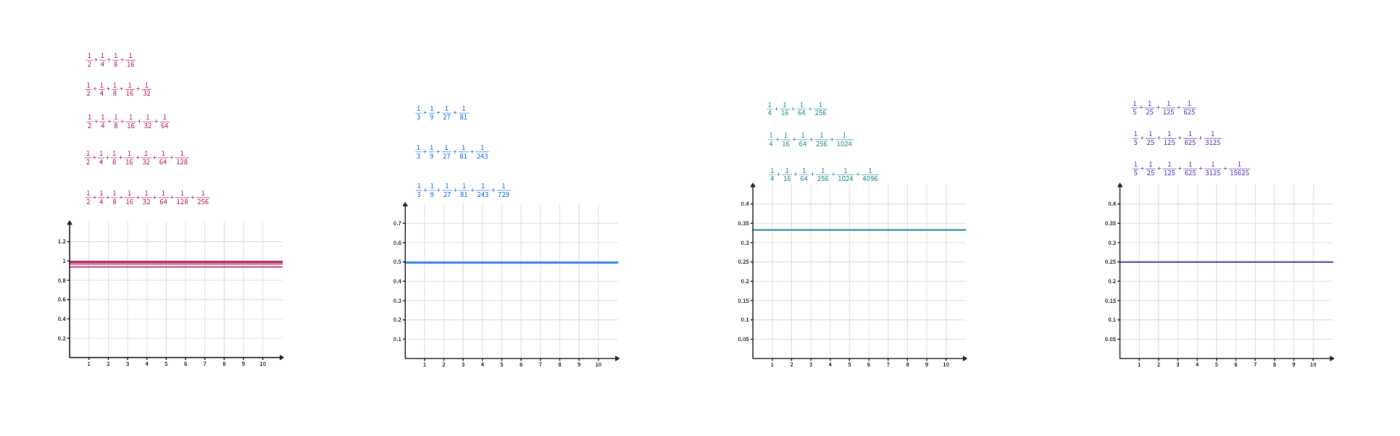
Ask them to predict what happens to the sums if they can continue adding each fraction's powers till infinity.
Main Activity
Start by inviting students to share their predictions about each infinite sum. Then, share this canvas with the students to let them work the geometric representations of different infinite sums
In the example of s, we used a 16 x 16 square to divide it into halves first; then we used the custom polygon tool to mark the piece of , then , and so on. There are several ways of doing so. Here we have two different ways of showing the infinite sum of is 1.
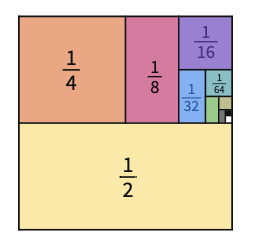
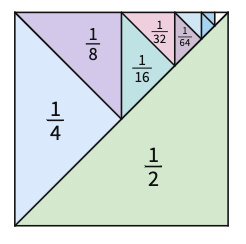
Let the groups work on the infinite sums of , , on the given squares.
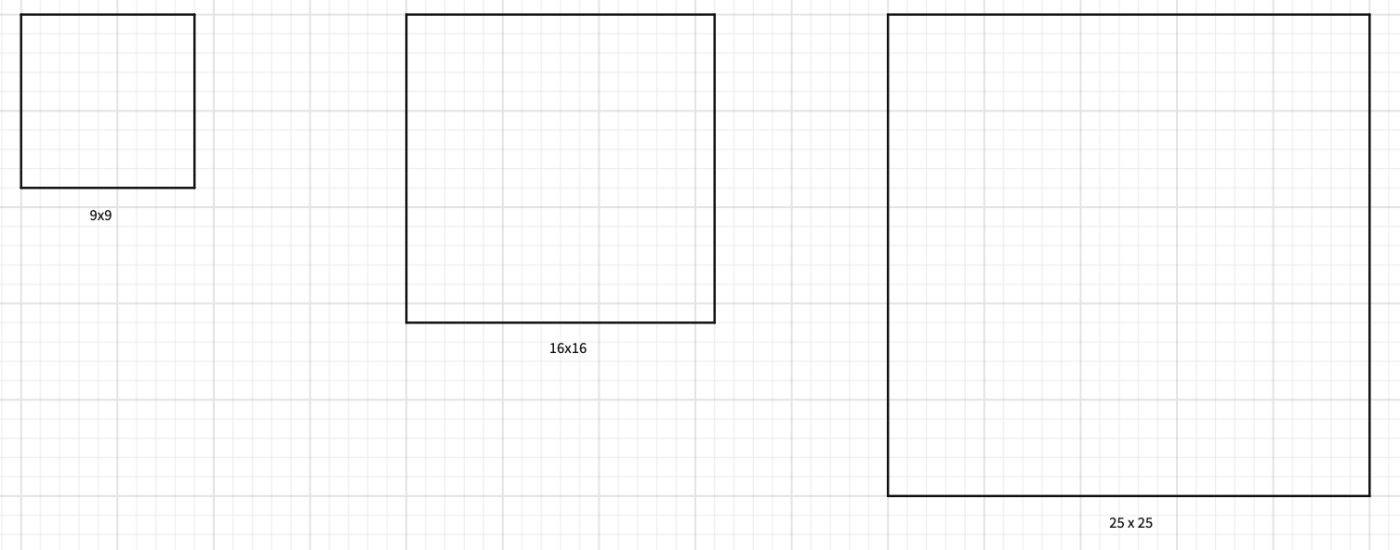
Some students may prefer to work on the coordinate plane, and some may need help with the custom polygon tool. For instance:
Some may use the area concept. Let's use the 9 x 9 square as an example again. There are 81 unit squares and the total number of unit squares colored by each power of is
Therefore the ratio of the areas is which is very close to
Closure
Share some student work with the class. Invite students to share which approaches they found most useful when answering these questions. Here are some possible representations.
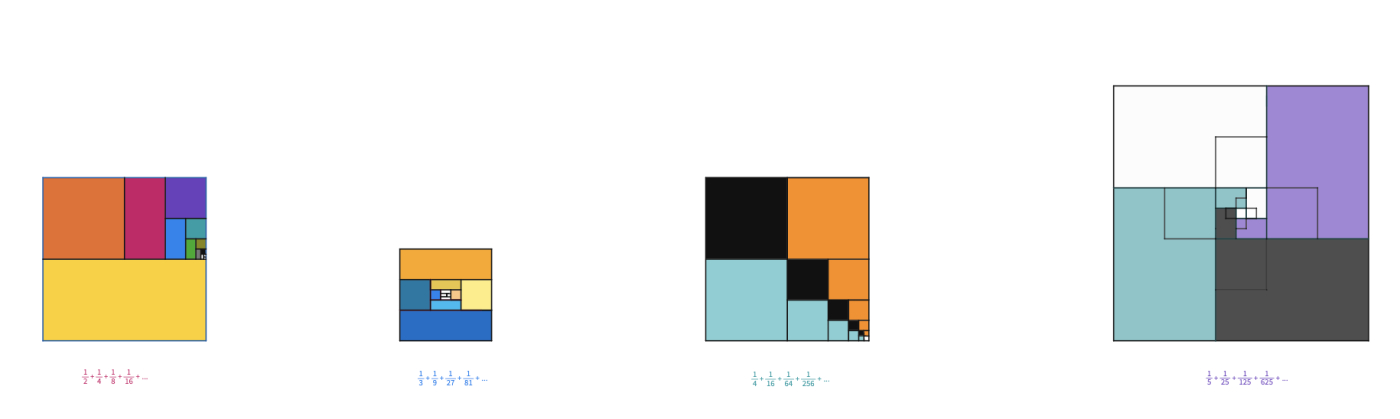
To close the lesson, ask students to find the infinite sum of where k >1. They may already notice the pattern; if not, encourage them the create a table to record their findings of each sum

Support and Extension
For students ready for additional extension in this lesson, consider asking the sum of
You may make a demonstration using the harmonic series canvas to let them use the graphing option.
For students needing additional support with these ideas, let them use the graph option like a calculator to see the sums in each addition step.
Polypads for This Lesson
To assign these to your classes in Mathigon, save a copy to your Mathigon account.
Click here to learn how to share Polypads with students and how to view their work.