Main Activity
Polygons here are drawn on a square grid. They have dots on their perimeter (p) and often interior (i) ones as well. Let's find a relationship between "p", "I", and the area of the polygons.
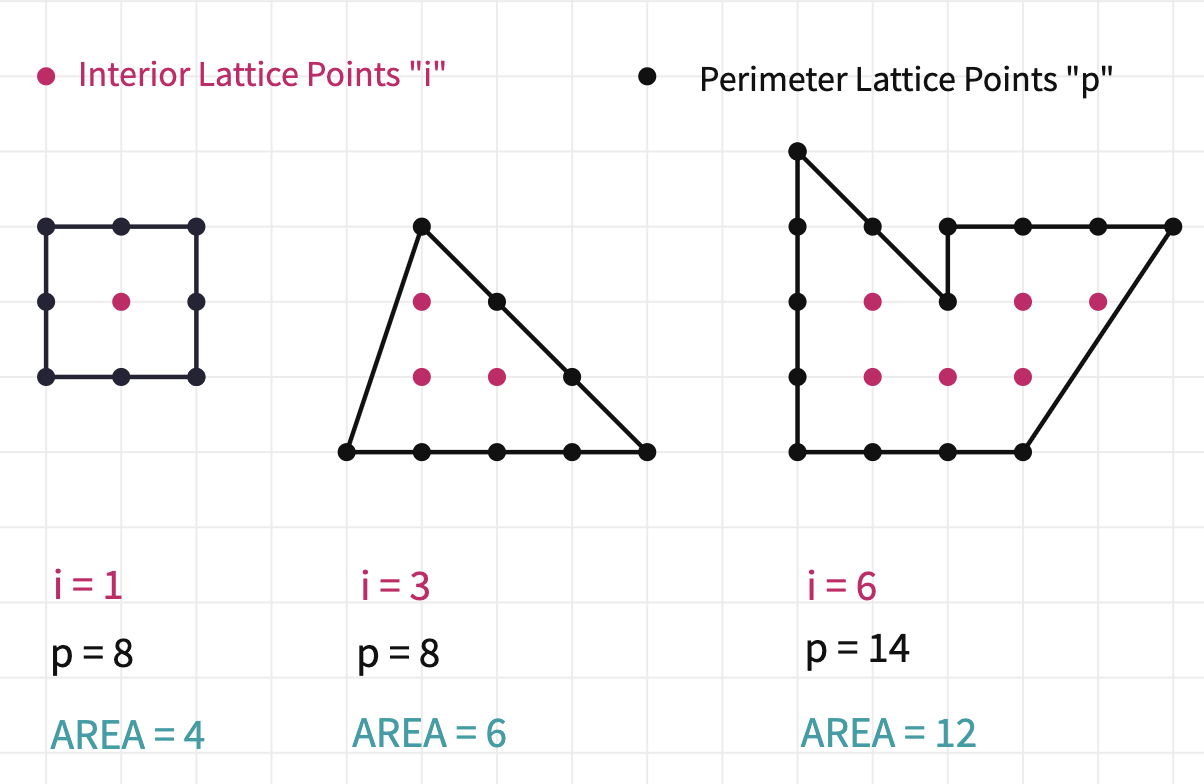
Try it out on an example;
To find the area you can use the irregular polygon tool to divide the enclosed region into triangles, squares, and rectangles. Here is one possible way of doing so;
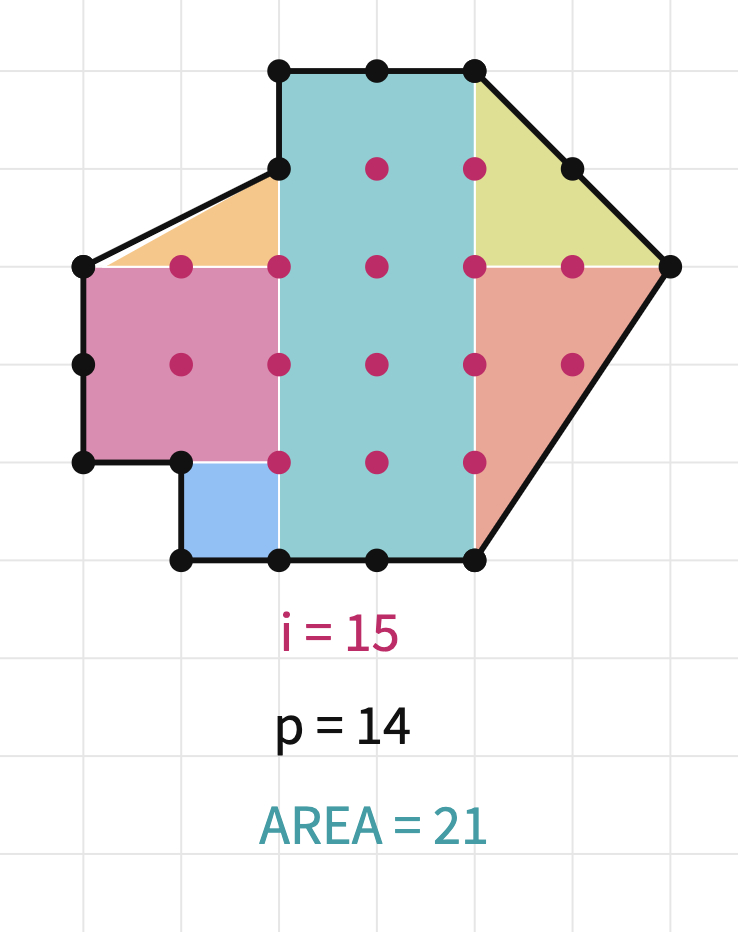
Finding a relationship among these three variables can be tricky.
Here are some other questions you can work on first:
Since there are three variables here, observing how two of the variables change while keeping one constant can be an effective strategy.
Think about these questions:
- How many different figures can be created with 4 perimeter points and no interior points? What do you notice about them?
- What do you notice about those figures whose areas are the same?
- What ways are there of increasing the area by 1 unit?
You can use the canvas here to draw as many figures as you want and keep a record of their number of perimeter points (p), interior points (i), and areas (A).
You can choose particular values for "p", and "i" and explore different shapes.
Try to create shapes to answer these questions;
- As the number of points on the shape's perimeter increases by one, what happens to area?
- As the number of interior points increases by one, what happens to area?
Solution
As mentioned before when there are three variables, observing how two of the variables change while keeping one constant can be an effective strategy.
Keep the number of perimeter points constant and increase the number of interior points one each time.
You may draw additional shapes to reach a conclusion about how the area increases by the number of interior points.
As the number of points on the shape's perimeter increases by one, the area increases by half.
This time, keep the number of interior points constant and increase the number of perimeter points one each time.
You may draw additional shapes to reach a conclusion about how the area increases by the number of perimeter points.
As the number of interior points increases by one, the area also increases by one.
Now we can build the relation on our observations: