ФракталыВведение

В природе вы могли встречать сложные растения, например как эти:

Этот папоротник состоит из множества маленьких листиков-веточек, которые соединяются в более крупные.

Этот брокколи Романенко состоит из небольших , закрученных по спирали вокруг большого.

Изначально они выглядят как очень сложные формы, но если вы посмотрите ближе, то сможете заметить, что они построены по относительно простому шаблону: все отдельно взятые части растений выглядят точно так же, как и всё растение целиком. Одна и та же картина повторяется снова и снова, только в больших масштабах.

В математике мы называем это свойство самоподобием, а формы, которые имеют это свойство, называются фракталами. Фракталы являются одними из самых красивых и самых странных объектов во всей математике.

Чтобы создать наши собственные фракталы, мы должны начать с простого шаблона, а затем повторять его снова и снова, в меньших масштабах.

Одним из самых простых шаблонов может быть линейный сегмент, добавим еще два сегмента на одном конце. Если мы повторим этот шаблон, оба этих синих сегмента также будут иметь две ветви на конце.

Вы можете перемещать синие точки, чтобы изменить длину и угол ветвей. Затем увеличьте количество итераций, используя ползунок ниже.

В зависимости от положения веток вы можете создавать совершенно разные рисунки - например, , или . Что еще вы сможете построить?

Другой известный фрактал - это треугольник Серпинского. В этом случае мы начинаем с большого равностороннего треугольника, затем делим его на четыре одинаковых треугольника и вырезаем центральный из них.

Обратите внимание, что окончательная форма состоит из трех идентичных копий себя, и каждая из них состоит из еще меньших копий большого треугольника! Вы можете продолжать увеличивать масштаб в треугольнике навсегда, а картинка и формы всегда будут повторяться.

Растения в начале этой главы выглядят точно так же, как фракталы, но мы понимаем, что невозможно создать бесконечные фракталы в реальной жизни. Если мы будем повторять один и тот же шаблон снова и снова, все в меньшем и меньшем масштабе, то мы в конечном итоге получим кусочки меньше клетки, молекулы или атома, которые мы больше не сможем разделить.

Однако, в математике мы можем размышлять о свойствах, которыми могли бы обладать реальные фракталы - в этом и есть прелесть математики…

Фрактальная размерность

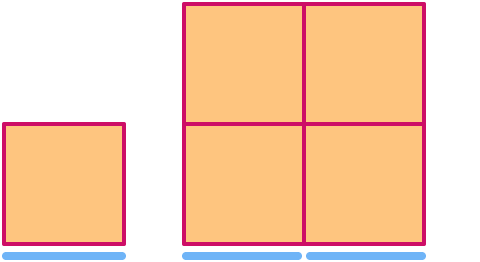
Во-первых, давайте подумаем о размерности фракталов. Линия имеет размерность . При увеличении в 2 раза его длина увеличивается в 21=2. Очевидно!

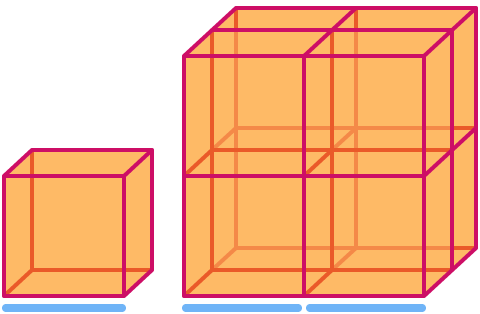
Квадрат имеет размерность . При масштабировании в 2 раза его площадь увеличивается в 22= .

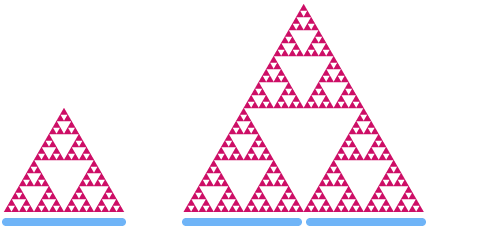
Куб имеет размерность . При увеличении в 2 раза его объем увеличивается в 23= . Заметьте, что больший куб на картинке состоит из 8 маленьких!

Теперь давайте посмотрим на треугольник Серпинского. Если мы масштабируем его в 2 раза, вы можете видеть, что его «площадь» увеличивается в раза.

Пусть d - это размерность треугольника Серпинского. Повторив те же действия, что и выше, мы получаем 2d=3. Другими словами, d = ≈ 1,558 ...

Но подождите ... как что либо может иметь измерение, которое не является целым числом? Это кажется невозможным, но это только одно из странных свойств фракталов. Фактически, это то, что дает фракталам их имя: они имеют дробное измерение (fraction - дробь).

Во время построения треугольника Серпиноского при каждой итерации мы удаляли часть площади треугольника. Если бы мы продолжили делать это бесконечно много раз, то удалили бы всю площадь: вот почему треугольник Серпинского - это нечто среднее между 2-мерной областью и 1-мерной линией.

Хотя многие фракталы являются самоподобными, все равно лучшее определение фрактала состоит в том, что фрактал это форма, которая имеет нецелую размерность.

Снежинка Коха

В природе мы встречаем много форм, которые выглядят как фракталы. Мы уже видели некоторые растения в начале этой главы. Другими замечательными примерами являются снежинки и ледяные кристаллы:

Чтобы создать нашу собственную фрактальную снежинку, нам снова нужно придумать простую последовательность действий, которую мы можем повторять снова и снова.

Как и в треугольнике Серпинского, давайте начнем с одного равностороннего треугольника. Однако вместо вырезания внутренней части, мы будем достраивать уменьшенные треугольники на каждой стороне. Длина стороны достроенного треугольника равна от длины стороны треугольника на предыдущем шаге.

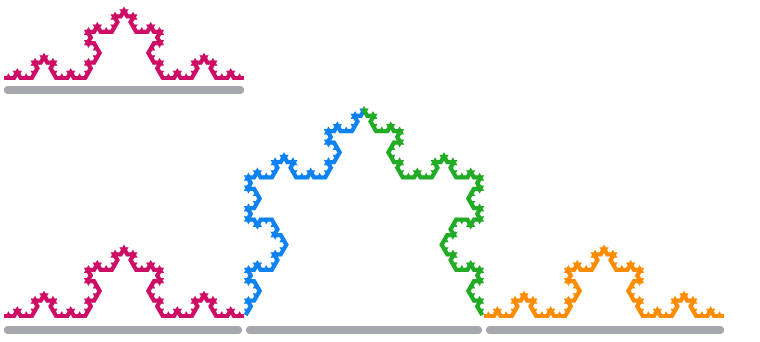
Получившаяся форма называется снежинка Коха, названная в честь шведского математика Хельге фон Кох. Еще раз обратите внимание, что маленький участок края снежинки выглядят точно так же, как большой участок.

Когда мы масштабируем один край снежинки Коха в 3 раза, его длина увеличивается .

Если снова мы захотим узнать, как меняется длина фрактала при масштабировании, то мы получим уравнение . Это означает, что размерность снежинки Коха равна d=log34≈1.262.

Площадь

Создание снежинок Коха похоже на рекурсивную последовательность: мы знаем начальную форму (треугольник) и знаем, как переходить к другому следующей (добавляя больше треугольников на каждом ребре):

новых треугольников

После первой итерации количество добавленных на этом шаге треугольников стало в раза больше. В то же время площадь этих новых треугольников уменьшается в раз с каждым шагом.

Предположим, что первый треугольник имеет площадь 1. Тогда общая площадь добавленных трех треугольников равна 3×19=13. Все последующие площади добавленных треугольников образуют , с коэффициентом .

Используя формулу для суммы бесконечной геометрической прогрессии, мы можем рассчитать, что общая площадь снежинки Коха равна

A=1+13×1=85=1.6.

Периметр

Мы также можем попытаться рассчитать периметр снежинки Коха. Как мы уже видели ранее, длина периметра увеличивается на коэффициент на каждом новом шаге.

Это означает, что мы снова имеем геометрическую прогрессию, но в этом случае она . Это означает, что периметр снежинки Коха на самом деле равен бесконечности!

Если это кажется нелогичным, просто представьте, мы умножаем периметр на 43 при каждой новой итерации и делаем это бесконечно много раз.

Почти немыслимо, что существует фигура с конечной площадью, но с бесконечным периметром - и это только одно из многих удивительных свойств фракталов.

Можете ли вы придумать свои собственные способы создания фракталов?

«Моя душа кружится морозными фракталами вокруг…»

Губка Менгера

Фракталы не обязательно должны быть «плоскими», как в примерах выше. Один из самых известных трехмерных фракталов это губка Менгера, названная в честь математика Карла Менгера, который впервые описал ее в 1926 году.

Мы начинаем с твердого куба и многократно просверливаем все меньшие и меньшие отверстия в его сторонах. Ширина вырезанного куба при каждой новой итерации составляет от ширины куба, вырезанного при предыдущей итерации.

Представим, что изначально куб состоял из 3×3×3=27 кубиков меньшего размера, потом мы удалили некоторые из них. Тогда Губка Менгера после первой итерации состоит из маленьких кубиков, ширина которых в 3 раза меньше первоначальной.

Теперь мы можем попытаться вычислить размерность d губки Менгера, как мы это делали для снежинки Коха выше. В этом случае мы получаем 3d=20 или d=log320≈2.727.

Если вы представите, что будете вырезать все больше и больше отверстий, бесконечно много раз, фактического объема не останется. Вот почему куб «не совсем» трехмерен!

Фрактальная береговая линия

Одна из ключевых характеристик всех фракталов, с которыми мы познакомились, состоит в том, что вы можете «увеличивать» их и всегда находить одинаковые паттерны. В 1920 г. британский математик Льюис Фрай Ричардсон понял, что то же самое работает с границами стран и береговыми линиям.

Вы начинаете с очертаний границы страны и, увеличивая масштаб, добавляете речные впадины, заливы и устья рек, затем отдельные скалы, камни, гальку и т.д.

Это серьезная проблема при попытке рассчитать длину границы страны - нужно решить, насколько сильно увеличивать масштаб, и включать укромные уголки и трещины?

Например, мы могли бы измерить длину береговой линии Великобритании, взяв длинную линейку, пройтись по ее берегу, а затем сложить все расстояния.

Если мы возьмем линейку длиной ${rulers[index]} км, то длина границы будет состоять из ${count} линеек, поэтому мы получаем длину береговой линии ${count} × ${rulers[index]} = ${count * rulers[index]} км.

Мы можем просто продолжать уменьшает длину линейки, и каждый раз наш результат длины береговой линии будет становиться немного больше. Как и у снежинки Коха, кажется, что береговая линия Британии имеет бесконечную длину! Это часто называют парадоксом береговой линии.

Несколько десятилетий спустя математик Бенуа Мандельброт наткнулся на работу Ричардсона в заброшенной библиотечной книге. Он осознал значение его работы, а также нашел связь с более поздними исследованиями фракталов и размерностей.

Береговая линия Британии, безусловно, выглядит как фрактал, но она не самоподобна, как другие фракталы, которые мы видели ранее. Чтобы найти ее размерность, мы можем поместить контур границы на сетке и подсчитать количество ячеек, которые она пересекла.

Первоначально мы получим 88 таких ячеек. Если мы увеличим береговую линию в 2 раза, то получим 197 ячеек - количество увеличилось больше чем в два раза!

Размер береговой линии увеличился в 19788. Как и раньше, это означает, что размерность береговой линии

d=log219788≈1.16

Если мы повторим это с более мелкими сетками, мы обнаружим, что размерность береговой линии Британии фактически равна 1,21. Мандельброт понял, что эта фрактальная размерность также является мерой шероховатости формы - новый показатель, который нашел приложение во многих других областях математики и физики.

Больше фракталов в природе и технике

Хотя идеальные фракталы никогда не могут появиться в природе, есть много объектов, которые выглядят почти как фракталы. Мы уже видели растения, снежинки и береговые линии, и вот еще несколько примеров:

Горный массив в Центральной Азии

Дельта реки Ганг в Индии

Молния

Кровеносные сосуды сетчатки глаза

Гранд-Каньон в США

Облака

Все эти объекты могли образоваться совершенно случайно, но, как и у фракталов, существует шаблон, по которому они формируются. Математика может помочь нам лучше понять формы, а фракталы находят применение в таких областях, как медицина, биология, геология и метеорология.

Компьютерная графика созданная с помощью фракталов

Мы также можем использовать фракталы для создания реалистичных «копий» природы, например, пейзажей и текстур, используемых в видеоиграх или компьютерных фильмах. Вода, горы и облака на этом изображении сделаны исключительно компьютером с помощью фракталов!

И мы можем даже использовать этот процесс, чтобы сжимать цифровые изображения, уменьшать их размер. Первые подобные алгоритмы были разработаны Майклом Барнсли и Аланом Слоаном в 1980-х годах, а новые до сих пор исследуются.

Изменить язык

Войдите в Mathigon

Поделиться

Сбросить прогресс

Глоссарий