ФракталыМножество Мандельброта

Все фракталы, которые мы видели в предыдущих главах, были созданы с использованием процесса повторения: вы начинаете с определенного шаблона, а затем повторяете его снова и снова.

Это похоже на другое понятие в математике, которое вы видели раньше: с рекурсивными последовательностями. Вы начинаете с определенного числа, а затем снова и снова применяете ту же рекурсивную формулу, чтобы получить следующее число.

Давайте возьмем рекурсивную формулу xn=xn−12 в качестве примера и нанесем ее члены на числовую прямую. Вы можете изменить значение x0:

Обратите внимание, что получившаяся последовательность может вести себя очень по-разному, в зависимости от начального значения x0:

Пока что мы не узнали ничего нового. Однако около ста лет назад математики начали исследовать, что происходит с этими последовательностями, если использовать в них комплексные числа, а не просто прямую действительных чисел. Их открытия были одними из самых удивительных и красивых результатов во всей математике.

Множества Жюлиа

Давайте использовать ту же последовательность, что и раньше, xn=xn−12, но в комплексной плоскости. Вы можете переместить позицию x0, чтобы увидеть, что происходит со следующими членами последовательности. Если последовательность будет сходиться, то мы будем закрашивать точку x0 на плоскости в синий цвет:

Как видите, последовательность сходится, пока x0 лежит внутри единичной окружностиснаружи единичного квадратана оси х (окружность с радиусом 1, центр в начале координат).

Теперь давайте немного усложним. Вместо того чтобы просто возводить в квадрат предыдущее число, мы также каждый раз будем добавлять константу c (это может быть любое комплексное число). Другими словами, xn=xn−12+c. Как вы думаете, мы по прежнему получим круг сходимости? Как вы думаете, какую форму мы сможем увидеть? Продолжить

На этой диаграмме вы можете менять позицию x0, а также значение c:

Все эти узоры, которые образуются на плоскости, называются Множества Жюулиа. Они были открыты независимо двумя французскими математиками, Гастоном Жюлией и Пьером Фату, около 1918 года.

В то время не было компьютеров, которые могли бы помочь построить визуальную модель, как на самом деле выглядят наборы Жюлиа. Математики, такие как Жюлиа и Фату, могли только математически рассуждать о них, но увидеть на практике можно было только грубые, нарисованные от руки наброски.

У нас сегодня такой проблемы нет - на изображениях ниже представлены разные наборы Жюлиа. Различные цвета указывают, насколько быстро последовательность в этой точке расходится:

Продолжить

Множество Мандельброта

При создании различных наборов Жюлиа вы могли заметить, что были некоторые значения c, для которых каждая последовательность расходится, и вся комплексная плоскость остается белой. Спустя несколько десятилетий после Жюлиа и Фату новое поколение математиков попыталось отобразить эти области на одном рисунке.

В предыдущем примере мы выбрали фиксированное значение для c, а затем меняли положение x0, чтобы раскрасить плоскость. Теперь давайте зафиксируем значение x0=0 и будем менять значение c.

Попробуйте еще раз поменять положение точки и нарисуйте область, в которой последовательности остаются ограниченными. Какую форму вы получите?

xn=xn−12+${complex(c)}

x0=${complex(x0)}

x1=${complex(x1)}

x2=${complex(x2)}

x3=${complex(x3)}

…Bounded!Diverges!

Этот фрактал называется Множеством Мандельброта, и при повороте на 90 ° он выглядит почти как человек с головой, телом и двумя руками. Впервые оно было определено и нарисовано в 1978 году в исследовательской работе математиков Роберта Брукса и Питера Мательски:

Несколько лет спустя Бенуа Мандельброт использовал мощные компьютеры в IBM, чтобы создать гораздо более детальную визуализацию фрактала, который впоследствии был назван его именем. Первые изображения на бумаге выглядели не так, как он ожидал - пока он не осознал, что специалисты, работающие с принтерами, убирали «размытость» по краям, предполагая, что это было вызвано частицами пыли или ошибками принтера, а не определяющей характеристикой фракталов! Продолжить

Как и все фракталы, мы можем «приближать» набор Мандельброта вечно, находя новые паттерны при любом масштабе. На изображении ниже вы можете увеличить часть множества Мандельброта, которая называется Морской конек. Черные точки, которые находятся внутри множества Мандельброта, показывают область, где последовательность ограничена. Цветные точки, которые находятся за пределами множества Мандельброта, где последовательность расходится, а разные цвета указывают как быстро она расходится:

Scale: ${pow(scale)}

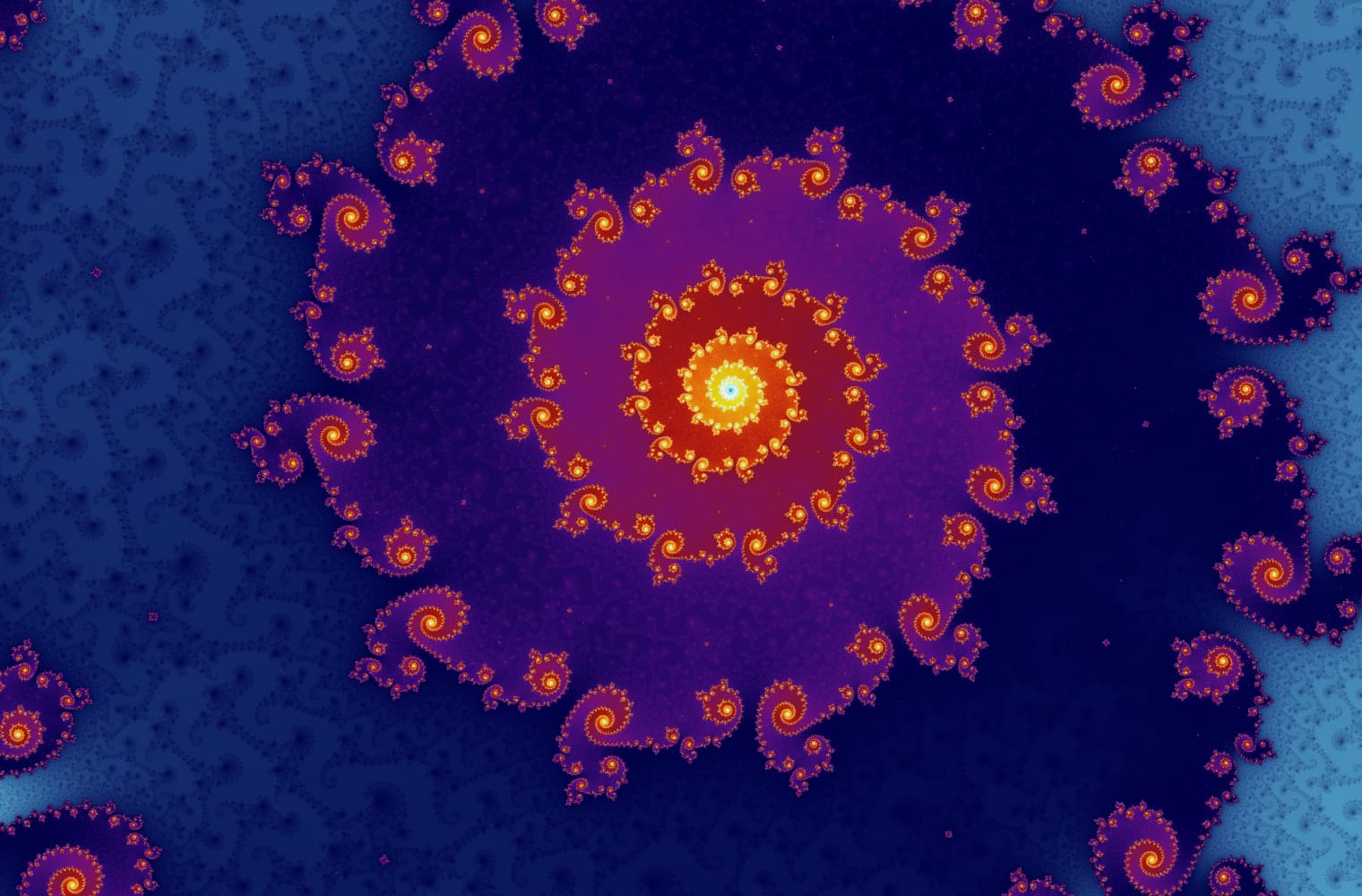
Этот слайд состоит из 27 отдельных изображений с уровнем увеличения более 14 квадриллионов или 254. В общей сложности на современном ноутбуке на рендер этого видео ушло бы почти 45 минут. Множество Мандельброта может быть создано с помощью одного простого уравнения xn=xn−12+c, но оно бесконечно сложно и потрясающе красиво.

По мере перемещения значения c по множеству Мандельброта вы можете заметить любопытное свойство:

• Все последовательности в главной кардиоиде множества Мандельброта сходятсярасходятсяимеют орбиты в одну точку.
• Последовательности внутри большого круга в верхней части имеют орбитысходятсярасходятся , состоящие из точек.
• Последовательности в этом меньшем круге имеют орбиты из точек.

В каждом круге последовательности имеют орбиты с разным количеством циклов, причем, чем меньше круг, тем больше циклов в орбитах. Размер этих орбит тесно связан с логистической картой, важной концепцией в теории хаоса.