Многоугольники и многогранникиЗамощение

Многоугольники встречаются в природе повсюду. Они особенно полезны, если мы хотим разбить большую площадь на части, потому что мы можем соединить многоугольники без зазоров или наложений. Такие действия называются замощением .

Люди скопировали эти природные паттерны в искусстве, архитектуре и технике - от древнего Рима до современности. Вот несколько примеров:

Здесь вы можете создавать свои собственные замощения, используя обычные многоугольники. Просто перетащите фигуры с боковой панели на холст. Какие формы хорошо соединяются? Есть ли какие-либо фигуры, которые вообще не замащиваются? Попробуйте создать интересные шаблоны!

Examples of other students’ tessellations

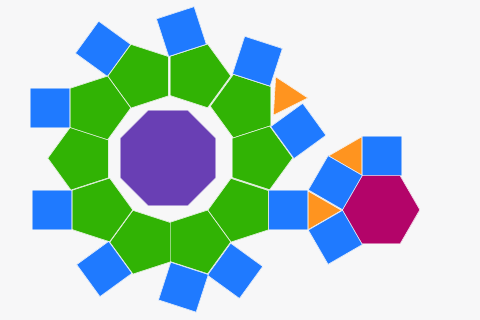
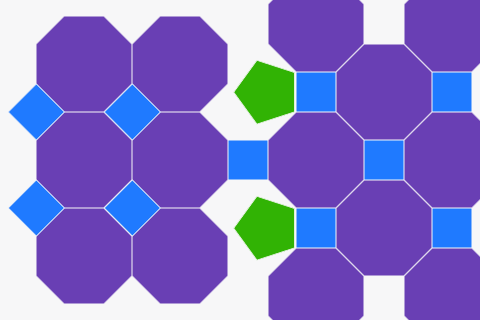
Замощение из правильных многоугольников

Вы могли заметить, что некоторые правильные многоугольники (например, квадратыпятиугольники ) замащиваются очень легко, в то время как другие (как пятиугольникитреугольникишестиугольники ) не получается замостить вообще.

Это связано с размером их внутренних углов , который мы научились вычислять ранее. В каждой вершине замощения встречаются внутренние углы нескольких разных многоугольников. Нам нужно, чтобы все эти углы в сумме давали °, иначе мы получим зазор, либо наложение.

Вы также можете проверить, что, как и пятиугольники, любой правильный многоугольник с 7 или более сторонами не замащивается. Это означает, что единственные правильные многоугольники, которые можно замостить, - это треугольники, квадраты и шестиугольники!

Конечно, вы можете комбинировать различные виды правильных многоугольников для замащивания, при условии, что их внутренние углы могут дать в сумме 360°:

Квадраты и треугольники
90° + 90° + 60° + 60° + 60° = 360°

Квадраты и треугольники
90° + 90° + 60° + 60° + 60° = 360°

Шестиугольники и треугольники
120° + 120° + 60° + 60° = 360°

Шестиугольники и треугольники
120° + 60° + 60° + 60° + 60° = 360°

Шестиугольники, квадраты и треугольники
120° + 90° + 90° + 60° = 360°

Восьмиугольники и квадраты
135° + 135° + 90° = 360°

Двенадцатиугольники и треугольники
150° + 150° + 60° = 360°

Двенадцатиугольники, шестиугольники и квадраты
150° + 120° + 90° = 360°

Замощение из неправильных многоугольников

Мы также можем попытаться сделать замощения из неправильных многоугольников - если мы будем осторожны при их расположении.

С пятиугониками немного сложнее. Мы уже видели, что правильные пятиугольники не замощаютсязамощаются , а как насчет неправильных?

Вот три разных примера замощения пятиугольниками. Они не являются правильными , но при этом они все равно являются 5-сторонними многоугольниками.

До настоящего времени математики нашли только 15 различных видов замощения с (выпуклыми) пятиугольниками - самый последний из которых был обнаружен в 2015 году. Никто не знает, есть ли другие, или эти 15 единственные…

Замощения в искусстве

Замощение - это и инструмент, и вдохновение для многих художников, архитекторов и дизайнеров - наиболее известного голландского художника MC Escher . Работа Эшера содержит странные, мутирующие существа, узоры и пейзажи:

Эти работы часто выглядят забавно и просто, но основные математические принципы здесь те же, что и раньше: углы, повороты и многоугольники. Если математика не верна, замощение не сработает!

“Metamorphosis II” by M. C. Escher (1940)

Мозаика Пенроуза

Все замощения, которые мы видели до сих пор, имеют одну общую черту: они являются периодическими . Это означает, что они состоят из повторяющегося шаблона, который повторяется снова и снова. Они могут продолжаться вечно во всех направлениях и везде будут выглядеть одинаково.

В 1970-х годах британский математик и физик Роджер Пенроуз открыл непериодические замощения - они все еще продолжаются бесконечно во всех направлениях, но никогда не выглядят одинаково. Это так называемые мозаики Пенроуза , и для создания одного из них нужно всего несколько видов многоугольников:

Пенроуз изучал замощения исключительно для забавы, но оказалось, что внутренняя структура некоторых реальных материалов (таких как алюминий) имеет сходный характер. Мозаики даже использовались на туалетной бумаге, потому что производители заметили, что непериодический узор можно свернуть без выпуклостей.