Многоугольники и многогранникиПлатоновы тела

В начале этого курса мы определили правильные многоугольники как особенно «симметричные» многоугольники, где все стороны и углы конгруэнтны. Мы можем сделать что-то подобное для многогранников.

В правильном многограннике все грани являются конгруэнтными правильными многоугольниками, и в каждой вершине встречается одинаковое количество граней. Многогранники с этими двумя свойствами называются Платоновыми телами , названными в честь греческого философа Платона .

Так как же выглядят платоновы тела и сколько их там? Чтобы сделать трехмерную фигуру, нам нужно как минимум грани, которые встречаются в каждой вершине. Давайте начнем с наиболее простого правильного многоугольника: равностороннего треугольника.

Семь или более треугольников в каждой вершине также не создают новых многогранников: вокруг вершины недостаточно места, чтобы поместить такое количество треугольников.

Это означает, что мы нашли Платоновых тела, состоящих из треугольников. Давайте перейдем к следующему правильному многоугольнику: квадрату.

Далее давайте попробуем поработать с пятиугольниками:

Если пятиугольника встречаются в каждой вершине, мы получаем додекаэдр . У него граней. («Додека» означает «двенадцать» по-гречески.)

Следующий правильный многоугольник - это шестиугольник:

Если три шестиугольника встречаются в каждой вершине, мы немедленно получаем замощениемногогранникшестигранник Поскольку места больше нет, кажется, что нет платоновых тел, состоящих из шестиугольников.

То же самое происходит и для всех правильных многоугольников с более чем шестью сторонами. Мы больше не получаем никаких трехмерных полигонов.

Это означает, что есть только платоновых тел! Давайте посмотрим на них всех вместе:

Обратите внимание, как число граней и вершин чередуютсяравны для куба и октаэдра , а также для додекаэдра и икосаэдра , в то время как число ребер остается неизменнымменяется . Эти пары платоновых тел называются двойственными многогранниками .

Мы можем превратить многогранник в двойственный ему, «заменив» каждую грань вершиной, а каждую вершину гранью. Эти анимации показывают, как это происходит:

Тетраэдр является двойственным самому себе. Поскольку у него одинаковое количество граней и вершин, их замена ничего не изменит.

Платон считал, что вся материя во Вселенной состоит из четырех элементов: воздуха, земли, воды и огня. Он думал, что каждый элемент соответствует одному из Платоновых тел, а пятый будет представлять вселенную в целом. Сегодня мы знаем, что существует более 100 различных элементов, которые состоят из атомов, а не многогранников.

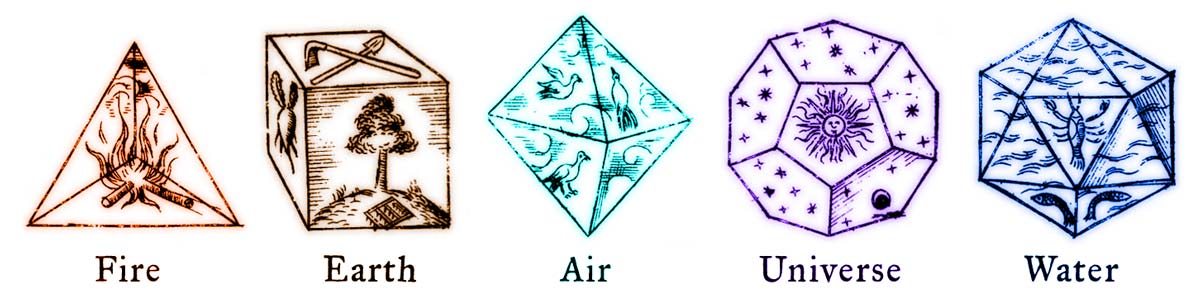
Изображение из книги Иоганна Кеплера “Harmonices Mundi” (1619)

Архимедовы тела

Платоновы тела являются особенно важными многогранниками, но существует множество других.

Например, архимедовы тела будут состоять из правильных многоугольников , но не обязательно из одних и тех же. Они названы в честь другого греческого математика, Архимеда Сиракузского , и их 13:

Применение

Платон ошибался, полагая, что все элементы состоят из платоновых тел. Но обычные многогранники обладают многими особыми свойствами, поэтому многогранники появляются в природе - и мы можем скопировать эти свойства в науке и технике.