Преобразования и симметрияГруппы симметрии и орнамента
Некоторые фигуры имеют более одной симметрии - давайте посмотрим на








Мы уже показали выше, что квадрат имеет
Он также имеет центральную симметрию на
И, наконец, мы можем думать о «бездействии» как о другом особом типе симметрии - потому что результат (очевидно) такой же, как и раньше. Это иногда называют тождеством.
В общей сложности мы нашли
Теперь мы можем начать делать некоторую арифметику с этими симметриями. Например, мы можем сложить две симметрии, чтобы получить новые:






Всякий раз, когда вы складываете две симметрии квадрата, вы получаете новый. Вот «калькулятор симметрии», где вы можете попробовать сделать это сами:
Потратьте некоторое время на игры с калькулятором симметрии и попробуйте найти любые шаблоны. Можете ли вы дополнить эти наблюдения?
- Сложение двух центральных симметрий всегда даст
симметрию (или тождество). - Сложение двух осевых симметрий всегда даст
симметрию (или тождество). - Сложение двух разных симметрий
. - Сложение с тождеством
.
Возможно, вы уже поняли, что сложение симметрий на самом деле очень похоже на сложение целых чисел:
- Сложение двух симметрий/целых чисел всегда дает другую симметрию/другое целое число:
+ = 12 + 7 = 19 - Сложение симметрий/целых чисел имеет
сочетательное свойство :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Любая симметрия/целое число имеет противоположную симметрию/противоположное целое число которое при сложении дает тождество или ноль:
+ = 4 + –4 = 0
В математике любой набор, который обладает этими свойствами, называется
В этом примере мы начали с восьми симметрий квадрата. Фактически, каждая геометрическая форма имеет свою собственную группу симметрии. Все они имеют разные элементы, но они всегда удовлетворяют трем правилам, расположенным выше.
Группы появляются везде в математике. Элементы могут быть числами или симметриями, но также полиномами, перестановками, матрицами, функциями. Ключевая идея теории групп заключается в том, что нас не интересуют отдельные элементы, только то, как они взаимодействуют друг с другом.
Например, группы симметрии разных молекул могут помочь ученым предсказать и объяснить свойства соответствующих материалов. Группы также можно использовать для анализа выигрышной стратегии в настольных играх, поведения вирусов в медицине, различных гармоний в музыке и многих других концепций…
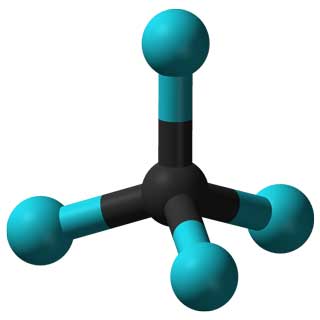
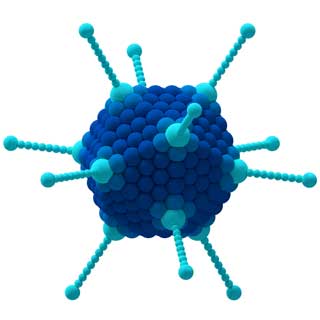
Свойства молекулы CCl4 (слева) и аденовируса (справа) определяются их симметрией.
Группы орнаментов
В предыдущих разделах мы познакомились с двумя видами симметрии, соответствующих двум разным преобразованиям: повороты и отражения. Однако, также существует симметрия для третьего вида изометрического преобразования:


Шестиугольные соты


Настенная керамическая плитка
В дополнение к осевой, центральной и симметрии переноса существует даже четвертый тип:


Орнамент может иметь более одного типа симметрии. И так же, как для квадратов, мы можем найти
Эти группы вряд ли покажут нам, как орнамент выглядит (например, его цвет и формы), но он может показать, как эти формы повторяются. Несколько разных орнаментов могут иметь одну и ту же группу симметрии, потому что узоры в них располагаются и повторяются одинаково.


Эти две модели имеют одинаковую симметрию, даже если они выглядят очень по-разному. Но симметрия не зависит от цвета или фигур.


Эти два шаблона также имеют одинаковую симметрию - даже если они выглядят более похожими на соответствующие орнаменты слева, чем друг на друга.
Хотя, существует бесконечно много возможных вариантов узоров, оказывается, что все они имеют одну из 17 различных групп симметрии. Они называются Группами орнаментов. Каждая группа орнаментов определяется сочетанием осевых, центральных, скользящих и симметрий переноса. Сможете ли вы увидеть

Type P1
Only translations

Type P2
Rotations of order 2, translations

Type P3
Rotations of order 3 (120°), translations

Type P4
Four rotations of order 2 (180°), translations

Type P6
Rotations of order 2, 3 and 6 (60°), translations

Type PM
Parallel axes of reflection, translations

Type PMM
Perpendicular reflections, rotations of order 2, translations

Type P4M
Rotations (ord 2 + 4), reflections, glide reflections, translations

Type P6M
Rotations (ord 2 + 6), reflections, glide reflections, translations

Type P3M1
Rotations of order 3, reflections, glide reflections, translations

Type P31M
Rotations of order 3, reflections, glide reflections, translations

Type P4G
Rotations (ord 2 + 4), reflections, glide reflections, translations

Type CMM
Perpendicular reflections, rotations of order 2, translations

Type PMG
Reflections, glide reflections, rotations of order 2, translations

Type PG
Parallel glide reflections, translations

Type CM
Reflections, glide reflections, translations

Type PGG
Perpendicular glide reflections, rotations of order 2, translations
К сожалению, нет простого объяснения, почему существует 17 этих групп. Доказательство требует гораздо более сложной математики ...
Вместо этого вы можете попробовать нарисовать свои собственные повторяющиеся узоры для каждой из 17 групп орнаментов:
Examples of other students’ drawings



Группы орнаментов были для плоских, двумерных узоров. Мы можем сделать нечто подобное для трехмерных моделей: они называются кристаллографическими группами, и их 219!
Помимо 4 симметрий для плоских фигур в эти группы входят симметрии, такие как симметрия плоскости скольжения и симметрия относительно винтовых осей (подумайте о движении при открытии бутылки с пробкой).
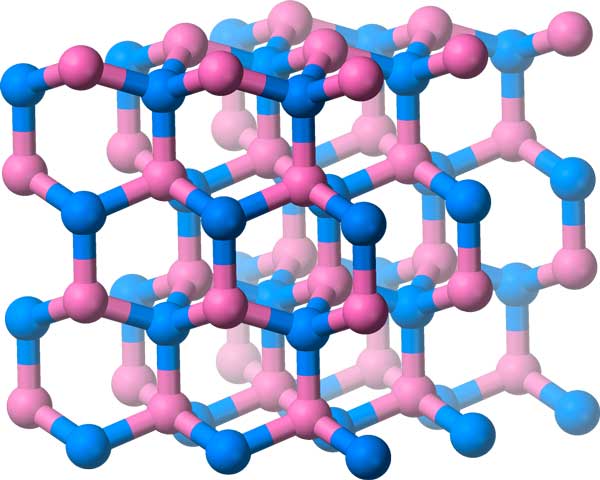
Нитрид бора имеет молекулы, расположенные в кристаллической решетке, которая имеет трехмерную группу симметрии.