Последовательности и паттерныАрифметические и геометрические прогрессии

В 1682 году астроном Эдмонд Галлей наблюдал необычное явление: светящийся белый объект с длинным хвостом, который двигался по ночному небу. Это была комета , маленький ледяной камень, который летит сквозь пространство, оставляя за собой след пыли и льда.

Галлей вспомнил, что другие астрономы наблюдали подобные кометы раньше: одну в 1530 году, а другую в 1606 году. Обратите внимание, что время между двумя последовательными наблюдениями одинаково в обоих случаях: лет.

Изображение Кометы Галлея,
сделана в 1986 на Острове Пасхи

Галлей пришел к выводу, что все три наблюдения были на самом деле одной и той же кометой, которая сейчас называется кометой Галлея . Она вращается вокруг Солнца и приближается к Земле примерно каждые 76 лет. Он также предсказал, когда комету можно будет увидеть снова:

1530, 1606*{span.arrow}+76*, 1682*{span.arrow}+76*, 1758*{span.arrow}+76*, +76, +76, +76, …

На самом деле, временной интервал не всегда составляет ровно 76 лет: он может меняться на один или два года, поскольку орбита кометы пересекается с другими планетами. Сегодня мы знаем, что комета Галлея наблюдалась древними астрономами еще в 240 году до нашей эры!

Описание кометы Галлея в разные времена: Вавилонская табличка (164 до н.э.), средневековый гобелен (1070г), научный журнал (1910г) и Советская почтовая марка (1986г).

Другая группа ученых исследовала поведение прыгающего теннисного мяча. Они сбросили мяч с высоты 10 метров и измерили его положение. С каждым отскоком мяч теряет часть своей первоначальной высоты:

Ученые заметили, что мяч теряет 20% своей высоты после каждого отскока. Другими словами, максимальная высота каждого отскока составляет 80% от предыдущего. Это позволило им прогнозировать высоту каждого следующего отскока:

10, 8*{span.arrow}×0.8*, ×0.8, ×0.8, 4.096*{span.arrow}×0.8*, 3.277*{span.arrow}×0.8*, 2.621*{span.arrow}×0.8*, 2.097*{span.arrow}×0.8*, …

Определения

Если вы сравните обе эти проблемы, вы можете заметить, что между ними есть много общего: частота появления кометы Галлея имеет одинаковую между годами появления, в то время как последовательность ударов теннисных мячей имеет одинаковое для соседних отскоков.

Последовательности с этими свойствами имеют специальное название:

Арифметическая прогрессия имеет постоянную разницу d между соседними членами.

Мы каждый раз прибавляем или вычитаем одно и то же число к каждому члену, чтобы получить следующий.

Геометрическая прогрессия имеет постоянное соотношение г между соседними членами.

Каждый новый член умножается или делится на одно и то же число, чтобы получить следующий.

Вот несколько разных последовательностей. Можете ли вы определить, какие из них являются арифметическими, геометрическими или ни одной из них, и каковы значения d и г ?

2 , 4 , 8 , 16 , 32 , 64 ,…

- это прогрессия с r = .

2 , 5 , 8 , 11 , 14 , 17 ,…

- это прогрессия с d = .

17 , 13 , 9 , 5 , 1 , –3 ,…

- это прогрессия с d = .

2 , 4 , 7 , 11 , 16 , 22 ,…

- это прогрессией .

40 , 20 , 10 , 5 , 2,5 , 1.25 ,…

- это прогрессия с r = .

Чтобы определить арифметическую или геометрическую прогрессию, мы должны знать не только d или r, но и первый член (а). Здесь вы можете создавать свои собственные последовательности и отображать их значения на графике, изменяя значения a , d и r . Можете ли вы найти какие-либо закономерности?

Арифметическая прогрессия

a = ${a} , d = ${d}

${arithmetic(a,d,0)}, ${arithmetic(a,d,1)}, ${arithmetic(a,d,2)}, ${arithmetic(a,d,3)}, ${arithmetic(a,d,4)}, ${arithmetic(a,d,5)}, …

Геометрическая прогрессия

a = ${b} , г = ${r}

${geometric(b,r,0)}, ${geometric(b,r,1)}, ${geometric(b,r,2)}, ${geometric(b,r,3)}, ${geometric(b,r,4)}, ${geometric(b,r,5)}, …

Обратите внимание, как все арифметические прогрессии выглядят очень похоже: если d положительно, они неуклонно , а если d отрицательно, то .

С другой стороны, геометрические прогрессии могут вести себя совершенно по-разному в зависимости от значений a и r :

Если r>1 члены быстро , до бесконечности. Математики говорят, что такая последовательность расходится .

Если r между –1 и 1 , то члены всегда будут , Мы говорим, что последовательность сходится .

Если r<−1 члены будут чередоваться с положительного на отрицательный, а их становиться больше.

Вы узнаете больше о схождении и расхождении в последнем разделе этого курса.

Рекурсивные и явные формулы

В предыдущем разделе вы узнали, что рекурсивная формула помогает найти значение каждого члена через значения предыдущих членов. Вот рекурсивные формулы для арифметической и геометрической прогрессии:

xn=

Проблема с рекурсивными формулами состоит в том, что, например, чтобы найти 100-й член, нам сначала нужно вычислить все предыдущие 99 - и это может занять много времени. Вместо этого мы можем попытаться найти явную формулу , которая напрямую выдает нам значение n- го члена.

Для арифметической прогрессии , мы должны прибавлять d на каждом новом шаге:

x1=a

x2=a+d

x3=a+d+d

x4=

x5=

Для нахождения n- ого члена мы прибавляем значений d, поэтому общая формула

xn=a+d×n−1

Для геометрические прогрессии , мы должны умножать на r на каждом новом шаге:

x1=a

x2=a×r

x3=a×r×r

x4=

x5=

Для нахождения n- ого члена мы умножаем раз на г, поэтому общая формула

xn=a×rn−1

Вот краткое изложение всех определений и формул, с которыми мы познакомились:

Арифметическая прогрессия имеет первый член a и каждый следующий член больше предыдущего на значение d - разности прогрессии.

Рекурсивная формула : xn=xn−1+d

Явная формула : xn=a+d×n−1

Геометрическая прогрессия имеет первый член a и каждый следующий член в r раз больше предыдущего (r - знаменатель прогрессии).

Рекурсивная формула : xn=xn−1×r

Явная формула : xn=a×rn−1

Теперь давайте посмотрим на некоторые примеры, где мы можем это использовать!

Заплати другому

Вот короткий отрывок из фильма «Заплати другому» , где 12-летний Тревор объясняет свою идею, как сделать мир лучше:

Суть идеи Тревора заключается в том, что, если все «заплатят другому», один человек может оказать огромное влияние на мир:

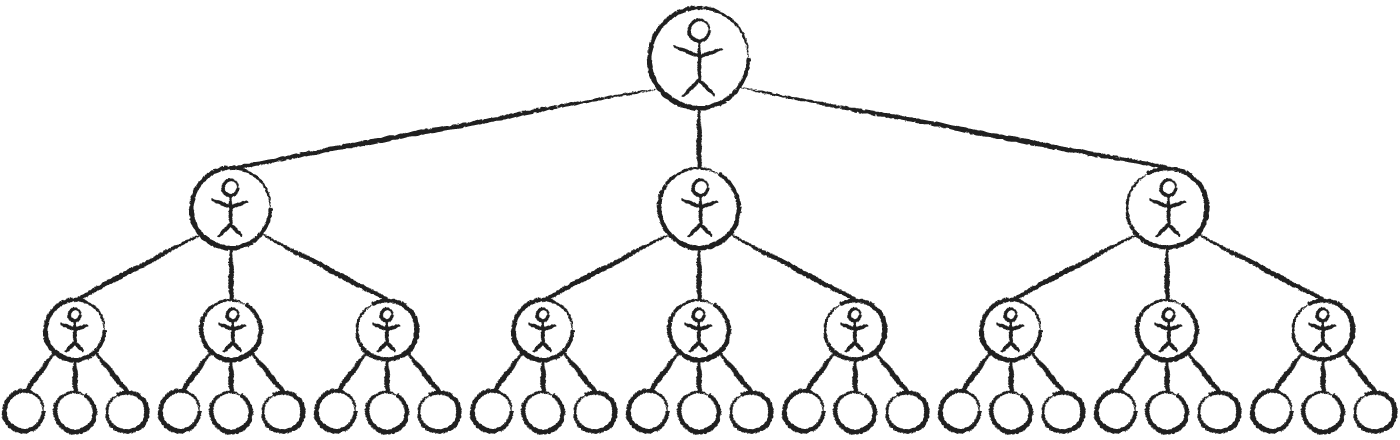
Обратите внимание, как количество людей на каждом шаге образует , со знаменателем :

1, 3*{span.arrow}×3*, 9*{span.arrow}×3*, ×3, ×3, ×3, …

Используя явную формулу для геометрических прогрессий, мы можем определить, сколько новых людей затронуто на каждом этапе:

xn =

Количество людей увеличивается невероятно быстро. На 10-м шаге вы достигнете количества 19 683 человек, а через 22 шага вы достигнете количества людей большего, чем в настоящее время живет на Земле.

Эта последовательность чисел имеет специальное имя: степени тройки . Как вы можете видеть, каждый член на самом деле представляет собой различную степень числа 3:

30 , 31 , 32 , 33 , 34 , 35 …

Кто хочет стать миллионером?

СКОРО БУДЕТ!

Проблема с шахматной доской

СКОРО БУДЕТ!

Изменить язык

Войдите в Mathigon

Поделиться

Сбросить прогресс

Глоссарий