Последовательности и паттерныЧисла Фибоначчи
Представьте, что вы получили пару маленьких кроликов, одного самца и одну самку. Это особенные кролики, они никогда не умирают, а самка рожает новую пару кроликов ровно раз в месяц (всегда другую пару мужского и женского пола).




















В первый месяц кролики слишком маленькие и не могут размножаться.
После первого месяца кролики подросли и могут начать размножаться…
… и после месяца у них рождается первая пара детей. Теперь у вас две пары кроликов.
На следующий месяц у вашей пары кроликов рождается еще пара крольчат. Тем временем первая пара крольчат растет. Теперь у вас три пары кроликов.
На пятый месяц у начальной пары кроликов рождается новая пара крольчат. В это же время из первая пара крольчат уже достаточно выросла, чтобы родить пару "правнуков". Теперь у вас пять пар кроликов.
На шестой месяц у вас есть три пары кроликов, у которых родятся крольчата: начальная пара, две пары их детенышей.
В следующем месяце у вас будет 13 пар кроликов: 8 из предыдущего месяца плюс 5 новых пар детенышей. Можете ли вы обнаружить закономерность в этой последовательности?
Количество кроликов в конкретном месяце равно
Можете ли вы рассчитать количество кроликов через несколько месяцев?
1, 1, 2, 3, 5, 8,
Таким образом, через 12 месяцев у вас будет 144 пары кроликов!
Эта последовательность чисел называется
Когда Фибоначчи родился в 1175 году, большинство людей в Европе все еще использовали
Вернувшись в Италию, Фибоначчи написал книгу под названием « Liber Abaci» (на латыни «Книга расчетов»), где он впервые ввел новые арабские цифры для европейских торговцев. Они имели незамедлительный успех - мы до сих пор пользуемся этой системой.
На одной из страниц своей книги он также исследовал схемы размножения кроликов - вот почему числа Фибоначчи были названы в его честь.
Pages from Fibonacci’s Liber Abaci
Конечно, числа Фибоначчи - это не то, как кролики на самом деле живут в реальной жизни. Кролики не рождают по два детеныша мужского и женского пола каждый месяц, и мы не учитывали, что кролики в конечном итоге умирают.
Но оказывается, что есть много других мест в природе, где числа Фибоначчи действительно появляются: например, спирали в растениях. Можете ли вы посчитать, количество спиралей в каждом направлении?
Эта шишка имеет
Этот подсолнух имеет 34 спирали по часовой стрелке и 55 спиралей против часовой стрелки.
В обоих случаях количество спиралей является последовательными числами Фибоначчи. То же самое верно и для многих других растений: в следующий раз, когда вы выйдете на улицу, посчитайте количество лепестков в цветке или количество листьев на стебле. Очень часто вы будет обнаруживать числа Фибоначчи!
Конечно, это не просто совпадение. Существует важная причина, почему природе нравится последовательность Фибоначчи, вы узнаете о ней позже.
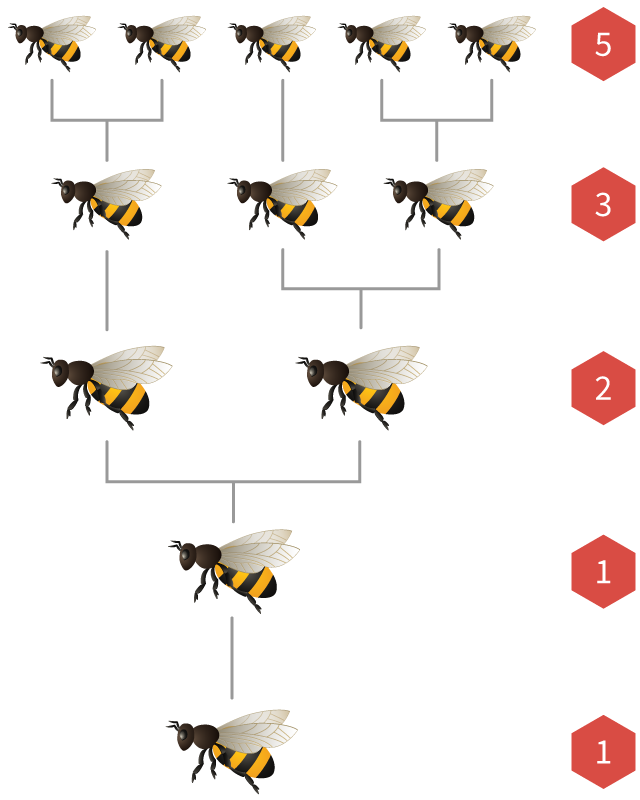
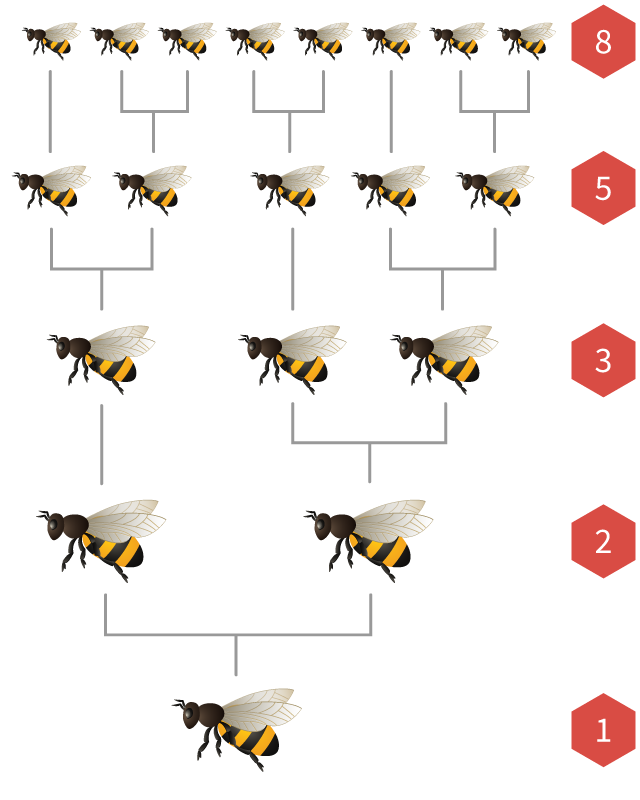
Числа Фибоначчи также появляются в популяциях пчел.
В каждой пчелиной колонии есть одна королева, которая откладывает много яиц. Если яйцеклетка оплодотворена самцом пчелы, из нее получается самка. Если яйцеклетка не оплодотворена, то получается самец (которого называют трутень).
Это означает, что у пчел женского пола есть
Если мы нарисуем генеалогическое древо пчел, число родителей, бабушек и дедушек, прабабушек и прародителей всегда будет числом Фибоначчи!
Иногда молодых самок пчел кормят специальной пищей, называемой «маточное молочко». В этом случае они становятся королевами и улетают, чтобы завести новый улей.
Золотое сечение
Как
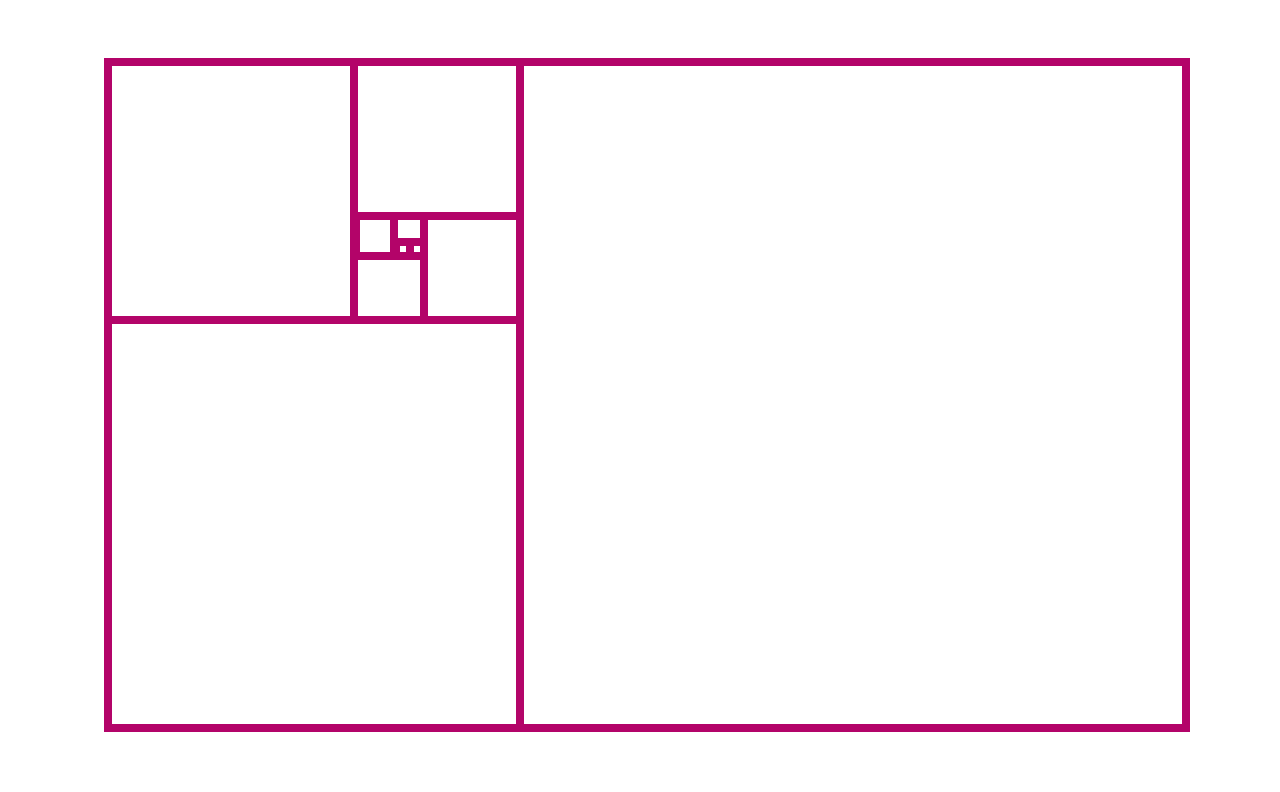
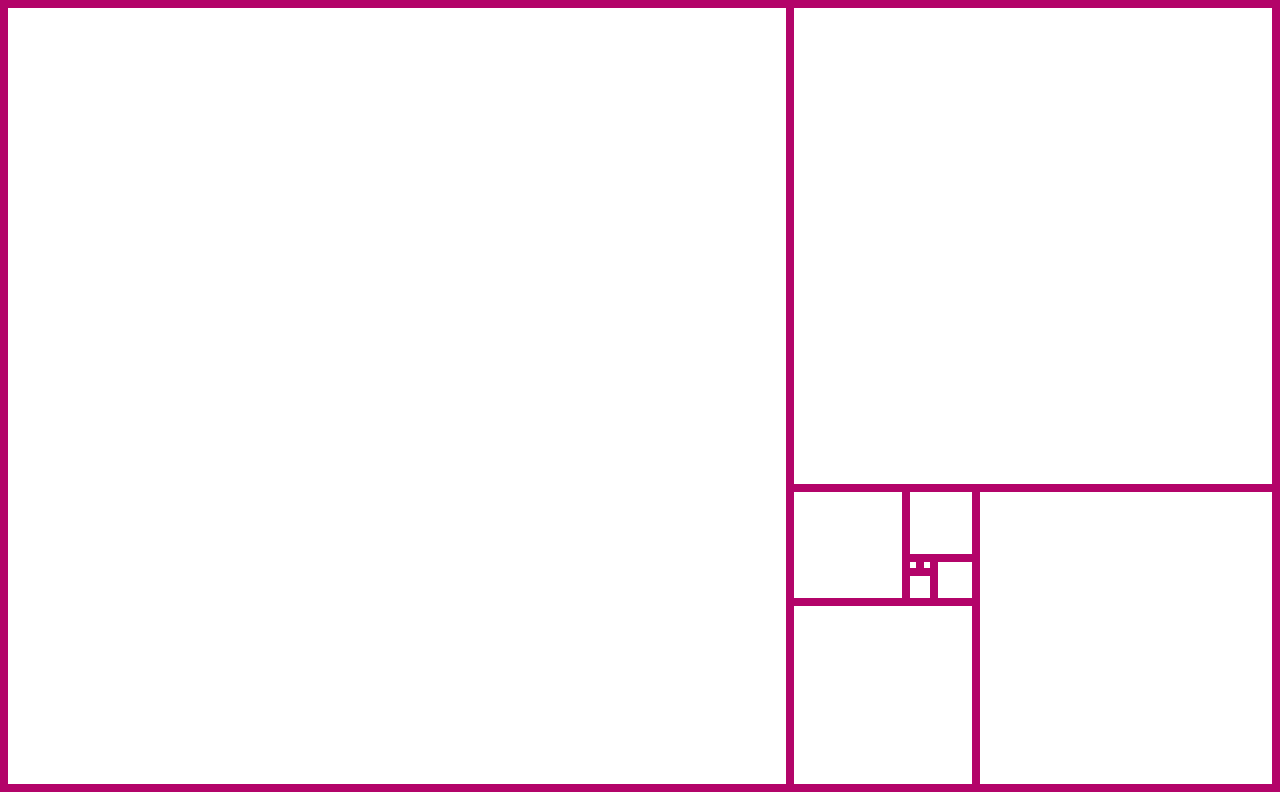
Мы начинаем с двух малых квадратов со стороной 1.
Дальше мы прибавляем квадрат со стороной 2, достраивая до большего прямоугольника.
Потом добавляем квадрат со стороной 3, формируя новый прямоугольник.
Следующий квадрат со стороной 5. Заметили, что все квадраты имеют стороны с длиной чисел Фибоначчи?
Если мы продолжим добавлять квадраты, они будут иметь длины сторон 8, 13, 21, и т.д.
Вы могли заметить, что чем больше становится прямоугольник, тем больше он становится похож на спираль. Мы даже можем визуализировать это нарисовав спираль, которая касается сторон квадратов.
На каждом шаге квадраты образуют больший прямоугольник. Его ширина и высота всегда являются двумя соседними числами Фибоначчи. Отношение сторон прямоугольника - это отношение его ширины и высоты:
Обратите внимание, что, когда мы добавляем все больше и больше квадратов, соотношение сторон кажется все ближе и ближе к определенному числу около 1,6. Это число называется
Многие люди считают, что золотое сечение особенно эстетично. Вот почему им часто пользуются художники и архитекторы - как в этих двух примерах:
Говорят, что греческий скульптор Фидий использовал золотое сечение при проектировании Парфенона в Афинах. Первая буква его имени,
«Тайная Вечеря» испанского художника Сальвадора Дали является одной из многих картин с золотым сечением. На заднем плане вы также можете увидеть большой
Мы можем получить золотое сечение
Однако оказывается, что точное значение
Спираль Фибоначчи
Золотое сечение объясняет, почему числа Фибоначчи появляются в природе, в подсолнечнике и сосновой шишке, которые вы видели в начале этого раздела.
Оба эти растения растут наружу от своего центра (часть растения, называемая меристема). Когда добавляются новые семена, листья или лепестки, они выталкивают уже существующие наружу.
Переместите ползунок вправо, чтобы увидеть, как растет растение. Обратите внимание, как каждый новый лист растет под другим углом в отличие от предыдущего. Угол между двумя последовательными листьями всегда одинаков.
Для цветов важно выбрать подходящий угол: листья или семена должны быть примерно одинаково отдалены друг от друга, чтобы они получали наибольшее количество солнечного света и питательных веществ. На диаграмме ниже вы можете посмотреть, как может выглядеть подсолнух под разными углами между его семенами:
Вы можете помнить, что отношение соседних чисел Фибоначчи становится все ближе и ближе к золотому сечению - и поэтому, если вы посчитаете количество спиралей в растении, вы часто будете находить число Фибоначчи.
Важно помнить, что природа не знает о числах Фибоначчи. Природа также не может решить уравнения для расчета золотого сечения, но в течение миллионов лет у растений было достаточно времени, чтобы опробовать разные углы и найти самый лучший.
Растения и животные всегда хотят расти наиболее эффективным способом, и поэтому природа полна регулярных математических моделей.
Fibonachos
До сих пор мы использовали только рекурсивное уравнение для чисел Фибоначчи. Существует также есть явное уравнение, но его гораздо сложнее найти:
Мы также можем попытаться выбрать разные начальные точки для чисел Фибоначчи. Например, если мы начнем с 2, 1, ..., а не с 1, 1, ..., мы получим последовательность, называемую числами Лукаса .
Получается, что какие бы два стартовых числа вы ни выбрали, результирующие последовательности имеют много общих свойств. Например, отношение соседних членов всегда будет
Есть много других головоломок, моделей и применений, связанных с числами Фибоначчи. Вот несколько примеров, которые вы можете попробовать сами:
Решение задач
1. Делимость чисел Фибоначчи
(а) Какие числа Фибоначчи четные? Есть ли правило, по которому они расположены в последовательности? Вы можете объяснить, почему?
(б) Какие числа Фибоначчи делятся на 3 (или делятся на 4)? Какие закономерности ты заметил?
2. Сумма чисел Фибоначчи
Что произойдет, если вы сложите три любых последовательных числа Фибоначчи? Вы можете объяснить, почему?
3. Лестницы Фибоначчи
Поднимаясь по лестнице, я могу либо сделать один шаг, либо перепрыгнуть через две ступени за раз. Это означает, что есть много разных возможностей для того, чтобы я мог подняться по лестнице. Например, если есть 5 ступеней, у меня есть 8 различных вариантов:
Сколько существует вариантов для лестницы с 6, 7 или 8 ступенями? Можете ли вы обнаружить закономерность? И как это связано с числами Фибоначчи?
© FoxTrot, by Bill Amend