Треугольники и тригонометрияСвойства треугольников
Начнем с простого: треугольник - это фигура с тремя сторонами (которые являются
Мы можем классифицировать треугольники по размеру их углов:
Прямоугольный треугольник имеет один
Тупоугольный треугольник имеет один
Остроугольный треугольник имеет
Для удобства мы всегда обозначаем треугольники по определенным правилам. Вершины обозначаем заглавными буквами A, B и C, стороны строчными буквами a, b и c, а углы греческими буквами
Сторона, которая лежит напротив вершины A, помечена как a, а угол, который находится рядом с A имеет маркировку
Медиана
Здесь вы можете увидеть треугольник, а также
Кажется, медианы всегда
Медианы всегда делят друг друга в соотношении 2: 1. Для каждой из трех медиан расстояние от вершины до центроида всегда
Центроид также является «точкой равновесия» или «центром тяжести» треугольника. Нарисуйте треугольник на картоне, вырежьте его и нарисуйте три медианы. Если вы были точны, то вы сможете уравновесить треугольник на кончике карандаша или повесить его на нити, прикрепленной к центроиду:
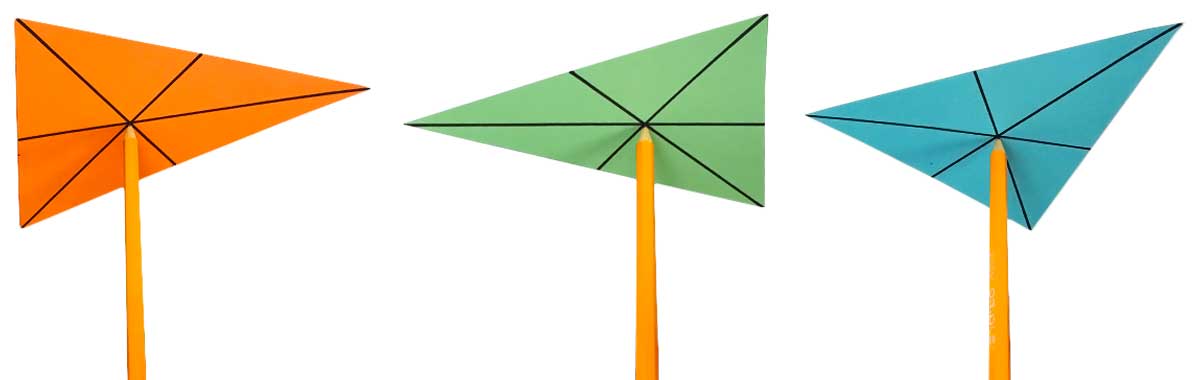
Это работает, потому что вес треугольника равномерно распределен вокруг центроида. В физике эту точку часто называют центром масс.
Срединные перпендикуляры и окружность
Напомним, что
Нарисуйте срединный перпендикуляр для всех трех сторон этого треугольника. Чтобы нарисовать срединный перпендикуляр, просто щелкните и проведите мышкой от одного конца отрезка до другого.
Как и прежде, три срединных перпендикуляра встречаются в одной точке. И опять же, эта точка обладает особым свойством.
Любая точка на срединном перпендикуляре расположена на одинаковом расстоянии от концов отрезка, который она делит пополам. Например, любая точка на синем срединном перпендикуляре имеет одинаковое расстояние от точек A и C, а любая точка на красном срединном перпендикуляре имеет одинаковое расстояние от точек
Точка пересечения лежит на всех трех срединных перпендикулярах, поэтому она должна располагаться на одинаковом расстоянии от всех трех
Это означает, что мы можем нарисовать окружность вокруг него, которая идеально проходит через все вершины. Эта окружность называется
Фактически это означает, что если вам даны три какие-либо точки, вы можете использовать срединные перпендикуляры, чтобы найти окружность, которая проходит через все три точки. (Только если точки не лежат на
Биссектриса и окружность
Вы, наверное, уже поняли логику: мы строим какой-то отрезок отрезок три раза для каждой стороны / угла треугольника, а затем выясняем, какими особенными свойствами обладает точка пересечения этих отрезков.
Напомним, что
Снова все три прямые пересеклись в одной точке. Вы, вероятно, ожидали этого, но важно заметить, что нет очевидной причины, по которой это должно происходить - треугольники - это просто особые формы!
Точки, лежащие на биссектрисе угла, находятся на одинаковом расстоянии от двух прямых, которые образуют угол. Например, любая точка на синей биссектрисе имеет одинаковое расстояние до стороны a и стороны c, также любая точка на красной биссектрисе имеет одинаковое расстояние до сторон
Точка пересечения лежит сразу на всех трех биссектрисах. Следовательно, она должна быть на одинаковом расстоянии от всех трех
Это означает, что мы можем построить окружность, которая лежит внутри треугольника и касается его трех сторон. Эта окружность называется вписанной в треугольник, а центр иногда называется инцентром.
Площадь и высота
Найти площадь
Ширина прямоугольника - это длина нижней стороны треугольника (которая называется основанием). Высота прямоугольника - это расстояние от основания до противоположной вершины.
Высота делит треугольник на две части - зеленую и оранжевую. Обратите внимание, что достроенные треугольники имеют ту же площадь, что и зеленый и оранжевый треугольники. Это означает, что площадь прямоугольника
Мы можем легко определить площадь прямоугольника, тогда площадь треугольника должна быть вдвое меньше:
Чтобы вычислить площадь треугольника, вы можете принять любую из трех сторон за основание, а затем найти соответствующую высоту, которая является отрезком, который
Каждый треугольник имеет
Как и
В
В