Треугольники и тригонометрияТеорема Пифагора

Мы дошли до важного момента в геометрии - возможности сформулировать и понять одну из самых известных теорем во всей математике: Теорему Пифагора. Он назван в честь древнегреческого математика Пифагора Самосского.

Теорема Пифагора В любом прямоугольном треугольнике квадрат длины гипотенузы (сторона, противоположная прямому углу) равен сумме квадратов двух других сторон. Другими словами,

a2 + b2 = c2

Обратное также верно: если три стороны в треугольнике удовлетворяют условию a2+b2=c2, то этот треугольник .

Прямые углы повсюду, и поэтому теорема Пифагора так полезна. На рисунке вы можете увидеть лестницу длиной 6 м, прислоненную к стене. Нижняя часть лестницы находится на расстоянии 1 м от стены. Как высоко вы сможете подняться по этой лестнице? Обратите внимание, что мы получили прямоугольный треугольник, образованный лестницей, стеной и землей. Используя теорему Пифагора, мы получаем

h2+12	=62
⇒h2	=
⇒h	=35=5.92м

Всякий раз, когда у вас есть прямоугольный треугольник, и вы знаете две его стороны, теорема Пифагора поможет вам найти третью.

Доказательство теоремы

Теорема Пифагора была известна древним вавилонянам, месопотамцам, индийцам и китайцам, но Пифагор, возможно, был первым, кто нашел математическое доказательство. На самом деле существует много разных способов доказать теорему Пифагора. Здесь вы видите три разных примера, каждый из которых использует свою стратегию:

Перестановка

Посмотрите на фигуру справа. Квадрат имеет длину стороны a + b, и он содержит четыре прямоугольных треугольника, а также меньший квадрат, который имеет площадь .

Теперь давайте переставим треугольники. В результате большой квадрат все еще содержит четыре прямоугольных треугольника, но теперь вместо одного квадрата мы имеем два квадрата с площадями .

Приравняв площадь розовой площади до и после перестановки, мы видим, что

a2+b2=c2.

Это оригинальное доказательство, которое использовал Пифагор.

c²

a²

b²

Алгебра

Здесь мы имеем ту же фигуру, что и раньше, только в этот раз мы будем использовать другой способ доказательства теоремы.

Длина стороны большого квадрата равна a+b и его площадь равна .

Квадрат состоит из четырех треугольников, каждый из которых имеет площадь , и один квадрат с площадью .

Если мы соединим всю эту информацию, мы получим

a+b2	=4×12ab+c2
a2+2ab+b2	=2ab+c2
a2+b2	=c2

И, снова, мы получим теорему Пифагора.

Подобные треугольники

Здесь вы можете увидеть произвольный прямоугольный треугольник. Если мы построим одну из высот этого треугольника, она разделит большой треугольник на два поменьше. Она также делит гипотенузу c на две маленьких отрезка, которые мы назовем x и y. Продолжить

Давайте рассмотрим два меньших треугольника отдельно, теперь проще заметить, что эти треугольники подобны… Прододжить

Оба меньших треугольника имеют равный угол с первоначальным треугольником. Также все три треугольника имеют прямой угол. По признаку подобия AA, все три треугольника должны быть .

Теперь мы можем использовать уравнения, которые мы уже знаем о подобных треугольниках:

xa=ac

x=a2c

yb=bc

y=b2c

Продолжить

Мы помним, что c = x + y. Поэтому

c=a2c+b2c

c2=a2+b2

Мы еще раз доказали теорему Пифагора!

О жизни Пифагора многое неизвестно, и ни одна оригинальная копия его работы не сохранилась. Он основал религиозный культ пифагорейцев, который практиковал своего рода «поклонение числам». Они считали, что все числа имеют свой собственный характер, и имели множество странных обычаев.

Пифагорейцам приписывают множество математических открытий, включая поиск первого иррационального числа 2. Иррациональные числа не могут быть выражены в виде обыкновенной дроби - концепция, которую пифагорейцы считали глубоко тревожной и (безуспешно) пытались скрыть!

Федор Бронников: «Пифагорейцы празднуют восход»

Расчет расстояний

Одним из наиболее важных применений теоремы Пифагора является расчет расстояний.

Справа вы видите две точки в системе координат. Мы могли бы измерить их расстояние с помощью линейки, но это будет не совсем точно. Вместо этого давайте попробуем использовать теорему Пифагора. Продолжить

Мы можем легко сосчитать горизонтальное расстояние вдоль оси x и вертикальное расстояние вдоль оси y. Если мы нарисуем эти две линии, мы получим прямоугольный треугольник.

Используя теорему Пифагора,

d2	=${b.x-a.x}2+${b.y-a.y}2
d2	=${(b.x-a.x)(b.x-a.x) + (b.y-a.y)(b.y-a.y)}
d	=${(b.x-a.x)2+(a.y-b.y)2}=${round(distance(a,b),4)}

Этот метод работает для любых двух точек:

Формула расстояния Если вам даны две точки с координатами (x1, y1) и (x2, y2), расстояние между ними составляет

d2=x2−x12+y2−y12

d=x2−x12+y2−y12

Пифагоровы Тройки

Перемещая вершины треугольника на предыдущем рисунке, вы, возможно, заметили, что в большинстве случаев длина гипотенузы d в конечном итоге была числом.

Однако есть несколько примеров прямоугольных треугольников, где длины всех трех сторон оказываются целыми числами.

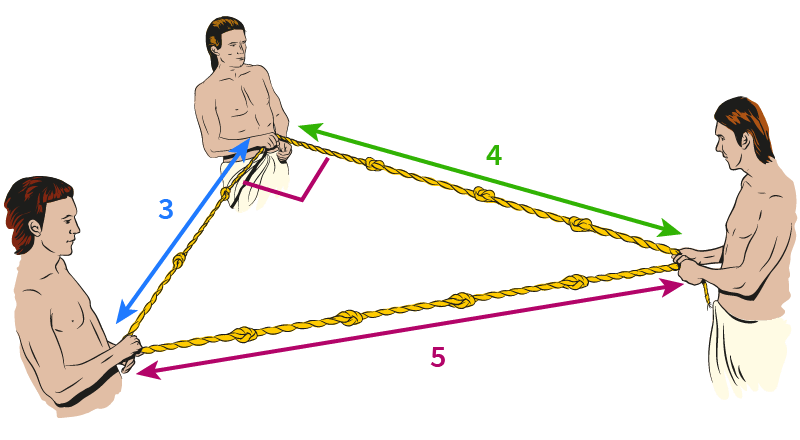
Один известный пример - треугольник со сторонами 3, 4 и 5. Так как 32+42=52, то любой треугольник со сторонами длины 3, 4 и 5 должен быть прямоугольным. Древние египтяне не знали о теореме Пифагора, но они знали о треугольнике 3-4-5. При строительстве пирамид они использовали веревки с узлами длиной 3, 4 и 5, чтобы строить идеальные прямые углы.

Три таких числа называются Пифагоровыми тройками. Числа (3, 4, 5) являются одним из примеров пифагоровых троек. Если мы умножим каждое число на 2, мы получим еще одну пифагорову тройку: (6, 8, ).

Мы можем рассматривать эти тройки как точки сетки в системах координат. Для пифагоровых троек расстояние от начала координат до точки сетки должно быть целым числом. Используя приведенную ниже систему координат, можете ли вы найти другие пифагорейские тройки?

${a.x}

${a.y}

${round(a.length,2)}

Вы заметили какие-то закономерности в расположении этих точек?

Изменить язык

Войдите в Mathigon

Поделиться

Сбросить прогресс

Глоссарий